请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。
(本小题满分10分)选修4—1:几何证明选讲
如图,⊙O是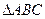 的外接圆,D是的中点,BD交AC于E。
的外接圆,D是的中点,BD交AC于E。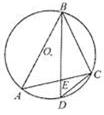
(I)求证:CD2=DE·DB。
(II)若 O到AC的距离为1,求⊙O的半径。
O到AC的距离为1,求⊙O的半径。
(本小题满分10分)
选修4—4:作标系与参数方程
已知直线 的参数方程为
的参数方程为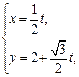 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为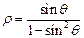 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线
,以极点为原点,极轴为x轴正半轴建立直角坐标系,M点坐标为(0,2),直线 与曲线C交于A,B两点。
与曲线C交于A,B两点。
(I)写出直线 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(II)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值。
(本小题满分10分)选修4—5:不等式选讲
设函数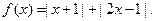
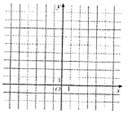
(I)画出函数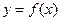 的图象;
的图象;
(II)若对任意 恒成立,求a-b的最大值。
恒成立,求a-b的最大值。
如图所示的几何体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的,
分别为
的中点,
分别为
,
的中点.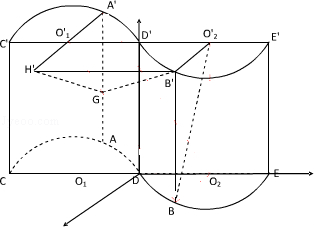
(1)证明:
四点共面;
(2)设
为
中点,延长
到
,使得
.证明:
平面
.
在某次测验中,有6位同学的平均成绩为75分.用
表示编号为
(
=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号 | 1 |
2 |
3 |
4 |
5 |
| 成绩
|
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩
,及这6位同学成绩的标准差
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
已知函数
.
(1)求
的值;
(2)设
.求
的值.
已知
为常数,且
,函数
,
(
=2.71828…是自然对数的底数).
(I)求实数
的值;
(II)求函数
的单调区间;
(III)当
=1时,是否同时存在实数
和
(
),使得对每一个
,直线
与曲线
都有公共点?若存在,求出最小的实数
和最大的实数
;若不存在,说明理由.
设函数
,其中,角
的顶点与坐标原点重合,始边与
轴非负半轴重合,终边经过点
,且
.
(Ⅰ)若点
的坐标为
,求
的值;
(Ⅱ)若点
为平面区域
上的一个动点,试确定角
的取值范围,并求函数
的最小值和最大值.