(本小题满分12分)
如图,多面体ABCD—EFG中,底面 ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下:
(I)求证:平面AEF⊥平面BDG;
(II)若存在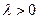 使得
使得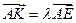 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为 ,求
,求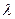 的值。
的值。
已知:函数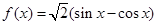 .
.
(1)求函数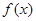 的最小正周期和值域;
的最小正周期和值域;
(2)若函数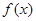 的图象过点
的图象过点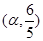 ,
,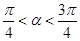 .求
.求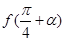 的值.]
的值.]
(本小题满分14分)已知函数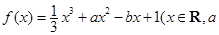 ,
,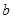 为实数)有极值,且在
为实数)有极值,且在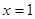 处的切线与直线
处的切线与直线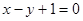 平行.
平行.
(Ⅰ)求实数a的取值范围;
(Ⅱ)是否存在实数a,使得函数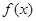 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(Ⅲ)设函数 ,试判断函数
,试判断函数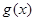 在
在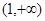 上的符号,并证明:
上的符号,并证明:
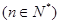 .
.
(本小题满分14分)如图,椭圆
 过点
过点 ,其左、右焦点分别为
,其左、右焦点分别为 ,离心率
,离心率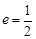 ,
, 是直x=上的两个动点,且
是直x=上的两个动点,且 .
.
(1)求椭圆的方程;
(2)求 的最小值;
的最小值;
(3)以 为直径的圆
为直径的圆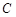 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.
(本小题满分14分)在单调递增数列 中,
中,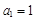 ,
, ,且
,且 成等差数列,
成等差数列, 成等比数列,
成等比数列,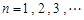 .
.
(1)分别计算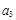 ,
, 和
和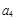 ,
,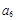 的值;
的值;
(2)求数列 的通项公式(将
的通项公式(将 用
用 表示);
表示);
(3)设数列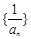 的前
的前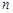 项和为
项和为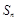 ,证明:
,证明: ,
,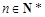
(本小题满分14分)如图,直角梯形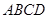 与等腰直角三角形
与等腰直角三角形 所在的平面互相垂直.
所在的平面互相垂直.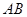 ∥
∥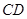 ,
,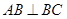 ,
, ,
,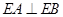 .
.
(1)求证: ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)线段 上是否存在点
上是否存在点 ,使
,使 // 平面
// 平面 ?若存在,求出
?若存在,求出 ;若不存在,说明理由.
;若不存在,说明理由.