(本小题满分14分)在单调递增数列 中,
中,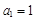 ,
, ,且
,且 成等差数列,
成等差数列, 成等比数列,
成等比数列,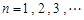 .
.
(1)分别计算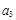 ,
, 和
和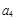 ,
,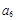 的值;
的值;
(2)求数列 的通项公式(将
的通项公式(将 用
用 表示);
表示);
(3)设数列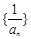 的前
的前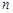 项和为
项和为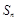 ,证明:
,证明: ,
,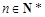
(本小题满分12分)已知公差大于零的等差数列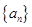 ,
,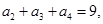 且
且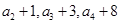 为等比数列
为等比数列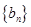 的前三项.
的前三项.
(1)求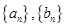 的通项公式;
的通项公式;
(2)设数列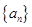 的前n项和为
的前n项和为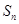 ,求
,求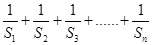 .
.
(本小题满分14分)已知函数 ,其中
,其中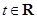 .
.
(Ⅰ)当 时,求曲线
时,求曲线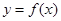 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求
时,求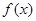 的单调区间;
的单调区间;
(Ⅲ)证明:对任意的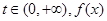 在区间
在区间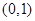 内均存在零点.
内均存在零点.
(本小题满分12分)已知A( ,0),B(
,0),B(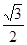 ,0)为平面内两定点,动点P满足|PA|+|PB|=2.
,0)为平面内两定点,动点P满足|PA|+|PB|=2.
(I)求动点P的轨迹方程;
(II)设直线 与(I)中点P的轨迹交于M、N两点.求△BMN的最大面积及此时直线l的方程.
与(I)中点P的轨迹交于M、N两点.求△BMN的最大面积及此时直线l的方程.
(本小题满分12分)已知数列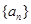 为等差数列,且
为等差数列,且 ,
, ;设数列
;设数列 的前
的前 项和为
项和为 ,且
,且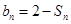 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若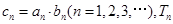 为数列
为数列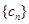 的前
的前 项和,求
项和,求
(本小题满分12分)设平面向量 = ( m , 1),
= ( m , 1), 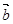 =" (" 2 , n ),其中 m, n
=" (" 2 , n ),其中 m, n  {-2,-1,1,2}.
{-2,-1,1,2}.
(I)记“使得 ⊥
⊥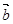 成立的( m,n )”为事件A,求事件A发生的概率;
成立的( m,n )”为事件A,求事件A发生的概率;
(II)记“使得 //(
//( -2
-2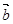 )成立的( m,n )”为事件B,求事件B发生的概率.
)成立的( m,n )”为事件B,求事件B发生的概率.