已知 ,用含有a、b的代数式表示
,用含有a、b的代数式表示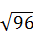 . (10’)
. (10’)
如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为BC的中点.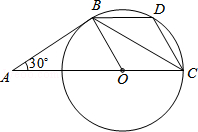
(1)求证:AB=BC;
(2)求证:四边形BOCD是菱形.
中国现行的个人所得税法自2011年9月1日起施行,其中规定个人所得税纳税办法如下:
一.以个人每月工资收入额减去3500元后的余额作为其每月应纳税所得额;
二.个人所得税纳税税率如下表所示:
| 纳税级数 |
个人每月应纳税所得额 |
纳税税率 |
| 1 |
不超过1500元的部分 |
3% |
| 2 |
超过1500元至4500元的部分 |
10% |
| 3 |
超过4500元至9000元的部分 |
20% |
| 4 |
超过9000元至35000元的部分 |
25% |
| 5 |
超过35000元至55000元的部分 |
30% |
| 6 |
超过55000元至80000元的部分 |
35% |
| 7 |
超过80000元的部分 |
45% |
(1)若甲、乙两人的每月工资收入额分别为4000元和6000元,请分别求出甲、乙两人的每月应缴纳的个人所得税;
(2)若丙每月缴纳的个人所得税为95元,则丙每月的工资收入额应为多少?
如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
某县为了了解2013年初中毕业生毕业后的去向,对部分初三学生进行了抽样调查,就初三学生的四种去向
| A.读普通高中; | B.读职业高中 | C.直接进入社会就业; | D.其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问: |
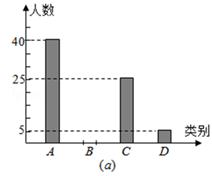
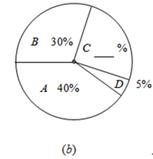
(1)该县共调查了 名初中毕业生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该县2013年初三毕业生共有4500人,请估计该县今年的初三毕业生中读普通高中的学生人数.
先化简,再求值: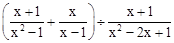 ,其中x=2.
,其中x=2.