 已知函数
已知函数 .
.
(1)用五点法画出它在 一个周期内的闭区间上的图象;
一个周期内的闭区间上的图象;
(2)指出 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;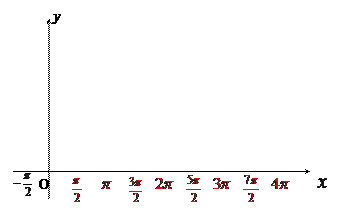 (3)说明此函数图象可
(3)说明此函数图象可 由
由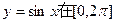 上的图象经怎样的变换得到.
上的图象经怎样的变换得到.
(本小题满分10分)
已知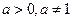 ,命题
,命题 函数
函数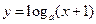 在
在 上单调递减,命题
上单调递减,命题 曲线
曲线
 与
与 轴交于不同的两点,若
轴交于不同的两点,若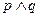 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围。
的取值范围。
(本小题10分)选修4-5:不等式选讲
设 ,试比较
,试比较 的大小
的大小
(本小题10分)选修4—4:坐标系与参数方程
已知某圆的极坐标方程为
(I)将极坐标方程化为普 通方程,并选择恰当的参数写出它的参数方程;
通方程,并选择恰当的参数写出它的参数方程;
(II)若点 在该圆上,求
在该圆上,求 的最大值和最小值.
的最大值和最小值.
(本小题10分)选修4—1:几何证明选讲
如图,设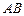 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径,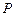 是⊙O与l的公共点,
是⊙O与l的公共点,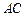 ⊥l,
⊥l,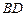 ⊥l,垂足分别为
⊥l,垂足分别为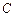 ,
, ,且
,且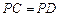 ,
,
求证:
(I)l是⊙O的切线;
(II)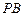 平分∠ABD.
平分∠ABD.
已知函数 ,
, 是
是 的一个零点,又
的一个零点,又 在
在 处有极值,在区间
处有极值,在区间 和
和 上是单调的,且在这两个区间上的单调性相反.
上是单调的,且在这两个区间上的单调性相反.
(I)求 的取值范围;
的取值范围;
(II)当 时,求使
时,求使
 成立的实数
成立的实数 的取值范围.
的取值范围.