(本小题10分)选修4-5:不等式选讲
设 ,试比较
,试比较 的大小
的大小
(本题满分10分)设圆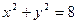 内有一点
内有一点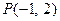 ,
,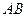 为过点
为过点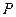 的直线。
的直线。
(1)当直线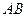 的倾斜角为
的倾斜角为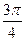 时,求弦
时,求弦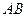 的长
的长
(2)当点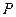 为弦
为弦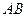 的中点时,求直线
的中点时,求直线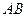 的方程
的方程
已知函数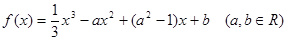 .
.
(Ⅰ)若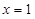 为
为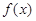 的极值点,求
的极值点,求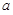 的值;
的值;
(Ⅱ)若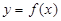 的图象在点(
的图象在点(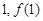 )处的切线方程为
)处的切线方程为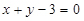 ,求
,求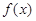 在区间
在区间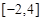 上的最大值;
上的最大值;
(Ⅲ)当 时,若
时,若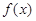 在区间
在区间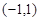 上不单调,求
上不单调,求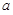 的取值范围.
的取值范围.
已知函数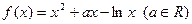 .
.
(I)若函数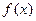 在
在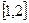 上是减函数,求实数
上是减函数,求实数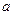 的取值范围;
的取值范围;
(II)令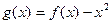 ,是否存在实数
,是否存在实数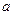 ,使得当
,使得当 时,函数
时,函数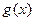 的最小值是
的最小值是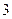 ,若存在,求出实数
,若存在,求出实数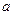 的值,若不存在,说明理由?
的值,若不存在,说明理由?
(III)当 时,证明:
时,证明: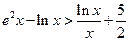 .
.
二次函数 满足
满足 。
。
(1)求函数 的解析式;
的解析式;
(2)在区 间
间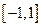 上,
上,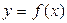
 的图象恒在
的图象恒在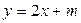 的图象上方,试确定实数
的图象上方,试确定实数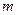 的取值范围。
的取值范围。
已知函数 最小正周期为
最小正周期为
(1)求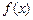 的单调递增区间
的单调递增区间
(2)在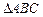 中,角
中,角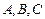 的对边分别是
的对边分别是 ,满足
,满足 ,求函数
,求函数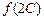 的取值范围
的取值范围