在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为线段BC的中点,E、F为线段AC的三等分点(如图①).将△ABD沿着AD折起到△AB′D的位置,连结B′C(如图②).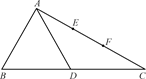
图①
图②
(1)若平面AB′D⊥平面ADC,求三棱锥B′-ADC的体积;
(2)记线段B′C的中点为H,平面B′ED与平面HFD的交线为l,求证:HF∥l;
(3)求证:AD⊥B′E.
棱长为1的正方体ABCD—A1B1C1D1中,P为DD1的中点,O1、O2、O3分别为平面A1B1C1D1、平面BB1C1C、平面ABCD的中心.
(1)求PO2的长。
(2)求证:B1O3⊥PA;
(3)求异面直线PO3与O1O2所成的角;
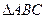 的三边a、b、c和面积S满足关系式:
的三边a、b、c和面积S满足关系式: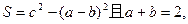 求面积S的最大值.
求面积S的最大值.
本题满分12分)
等差数列 的各项均为正数,
的各项均为正数,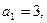 ,前n项和为
,前n项和为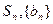 是等比数列,
是等比数列,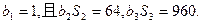
(1)求列数 和
和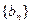 的通项公式;
的通项公式;
(2)求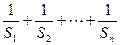 的值.
的值.
某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5,且相互之间无影响.
(1)求至少3个员工同时上网的概率;
(2)求至少几个员工同时上网的概率小于0.3?
(本小题满分14分)
已知圆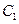 :
: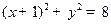 ,点
,点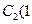 ,
, ,点
,点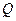 在圆
在圆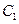 上运动,
上运动, 的垂直平分线交
的垂直平分线交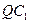 于点
于点 .
.
(Ⅰ)求动点 的轨迹
的轨迹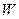 的方程;
的方程;
(Ⅱ)设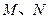 分别是曲线
分别是曲线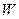 上的两个不同点,且点
上的两个不同点,且点 在第一象限,点
在第一象限,点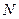 在第三象限,若
在第三象限,若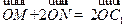 ,
,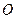 为坐标原点,求直线
为坐标原点,求直线 的斜率
的斜率 ;
;
(Ⅲ)过点 ,
,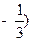 且斜率为
且斜率为 的动直线
的动直线 交曲线
交曲线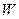 于
于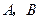 两点,在
两点,在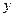 轴上是否存在定点
轴上是否存在定点 ,使以
,使以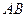 为直径的圆恒过这个点?若存在,求出
为直径的圆恒过这个点?若存在,求出 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.