(本小题满分12分)若对于正整数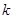 、
、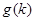 表示
表示
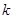 的最大奇数因数,
的最大奇数因数, 例如
例如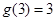 ,
,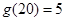 ,并且
,并且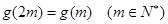 ,设
,设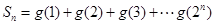
(1)求S1、S2、S3 ;
(2)求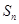 ;
;
(3)设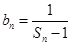 ,求证数列
,求证数列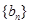 的前
的前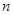 顶和
顶和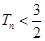 .
.
(本小题满分12分)如图 是图
是图 的三视图,三棱锥
的三视图,三棱锥 中,
中, ,
, 分别是棱
分别是棱 ,
, 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
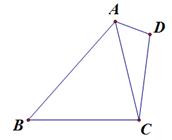
(本小题满分12分)如图所示,在四边形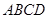 中,
中, ,且
,且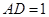 ,
,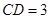 ,
,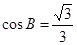 .
.
(1)求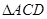 的面积;
的面积;
(2)若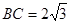 ,求
,求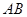 的长.
的长.
(本小题满分12分)某学校举行联欢会,所有参演的节目都由甲、乙、丙三名专业老师投票决定是否获奖.甲、乙、丙三名老师都有“获奖”、“待定”、“淘汰”三类票各一张.每个节目投票时,甲、乙、丙三名老师必须且只能投一张票,每人投三类票中的任何一类票的概率都为 ,且三人投票相互没有影响.若投票结果中至少有两张“获奖”票,则决定该节目最终获一等奖;否则,该节目不能获一等奖.
,且三人投票相互没有影响.若投票结果中至少有两张“获奖”票,则决定该节目最终获一等奖;否则,该节目不能获一等奖.
(1)求某节目的投票结果是最终获一等奖的概率;
(2)求该节目投票结果中所含“获奖”和“待定”票票数之和 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)如图,在斜三棱柱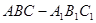 中,
中, 是
是 的中点,
的中点, ⊥平面
⊥平面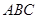 ,
, ,
,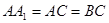 .
.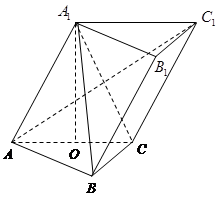
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
已知各项均不为零的数列 的前
的前 项和为
项和为 ,且
,且 ,其中
,其中 .
.
(1)求证: 成等差数列;
成等差数列;
(2)求证:数列 是等差数列;
是等差数列;
(3)设数列 满足
满足 ,且
,且 为其前
为其前 项和,求证:对任意正整数
项和,求证:对任意正整数 ,不等式
,不等式 恒成立.
恒成立.