如图,AB是半圆的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD。
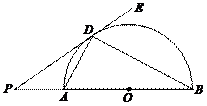
(1) 判断直线PD是否为⊙O的切线,并说明理由;
(2) 如果ÐBDE=60°,PD=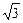 ,求PA的长。
,求PA的长。
如图,某仓储中心有一斜坡AB,其坡度为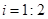 ,顶部A处的高AC为4m,B、C在同一水平地面上。
,顶部A处的高AC为4m,B、C在同一水平地面上。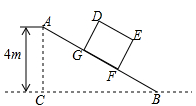
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方形货柜的侧面图,其中DE=2.5m,EF=2m.将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高。(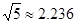 ,结果精确到0.1m)
,结果精确到0.1m)
已知二次函数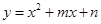 的图像经过点
的图像经过点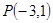 ,对称轴是经过
,对称轴是经过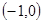 且平行于
且平行于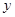 轴的直线。
轴的直线。
(1)求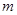 、
、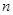 的值
的值
(2)如图,一次函数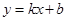 的图像经过点
的图像经过点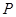 ,与
,与 轴相交于点
轴相交于点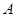 ,与二次函数的图像相交于另一点B,点B在点P的右侧,
,与二次函数的图像相交于另一点B,点B在点P的右侧,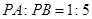 , 求一次函数的表达式。
, 求一次函数的表达式。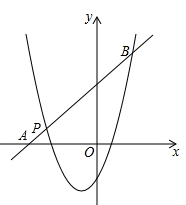
某校七年级社会实践小组去商场调查商品销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件, 并以每件120元的价格销售了400件.商场准备采取促销措施,将剩下的衬衫降价销售.请你帮商场计算一下,每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
一只不透明袋子中装有1个红球、2个黄球,这些球除颜色外都相同。小明搅匀后从中意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球。用画树状图或列表法列出摸出球的所有等可能情况,并求两次摸出的球都是红球的概率。
为了解学生参加社团的情况,从2010年起,某市教育部门每年都从全市所有学生中随机
抽取2000名学生进行调查.图①、图②是部分调查数据的统计图(参加社团的学生每人只能报一项,根据统计图提供的信息解决下列问题: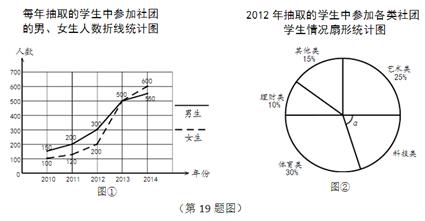
(1)求图②中“科技类”所在扇形的圆心角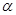 的度数;
的度数;
(2)该市 2012 年抽取的学生中,参加体育类与理财类社团的学生共有多少人?
(3)该市 2014 年共有 50000 名学生,请你估计该市2014年参加社团的学生人数.