如图，抛物线
与
轴相交于
、
两点（点在点的左侧），与
轴相交于点
，顶点为
.
（1）直接写出、、三点的坐标和抛物线的对称轴；
（2）连接
，与抛物线的对
称轴交于点
，点
为线段上的一个动点，过点作
交抛物线于点
，设点的横坐标为
；
①用含的代数式表示线段
的长，并求出当为何值时，四边形
为平行四边形？
②设
的面积为
，求与的函数关系式
在△ABC中，AB=AC，∠BAC=
（
），将线段BC绕点B逆时针旋转60°得到线段BD。
（1）如图1，直接写出∠ABD的大小（用含的式子表示）；
（2）如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；
（3）在（2）的条件下，连结DE，若∠DEC=45°，求的值。
在平面直角坐标系xOy中，抛物线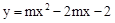
（
）与y轴交于点A，其对称轴与x轴交于点B。
（1）求点A，B的坐标；
（2）设直线l与直线AB关于该抛物线的对称轴对称，求直线l的解析式；
（3）若该抛物线在
这一段位于直线l的上方，并且在
这一段位于直线AB的下方，求该抛物线的解析式。
小明遇到这样一个问题：如图1，在边长为
的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠CHN=∠DEP=45°时，求正方形MNPQ的面积。小明发现：分别延长QE，MF，NG，PH，交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形（如图2）请回答：
（1）若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙，不重叠），则这个新的正方形的边长为；
（2）求正方形MNPQ的面积。参考小明思考问题的方法，解决问题：
（3）如图3，在等边△ABC各边上分别截取AD=BE=CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ，若
，则AD的长为。
第九届中国国际园林博览会（园博会）已于2013年5月18日在北京开幕，以下是根据近几届园博会的相关数据绘制的统计图的一部分：
（1）第九届园博会的植物花园区由五个花园组成，其中月季园面积为0.04平方千米，牡丹园面积为平方千米；
（2）第九届园博会园区陆地面积是植物花园区总面积的18倍，水面面积是第七、八两届园博会的水面面积之和，请根据上述信息补全条形统计图，并标明相应数据；
（3）小娜收集了几届园博会的相关信息（如下表），发现园博会园区周边设置的停车位数量与日接待游客量和单日最多接待游客量中的某个量近似成正比例关系，根据小娜的发现，请估计将于2015年举办的第十届园博会大约需要设置的停车位数量（直接写出结果，精确到百位）。
第七届至第十届园博会游客量与停车位数量统计表
| 日均接待游客量（万人次） |
单日最多接待游客量（万人次） |
停车位数量（个） |
|
| 第七届 |
0.8 |
6 |
约3 000 |
| 第八届 |
2.3 |
8.2 |
约4 000 |
| 第九届 |
8（预计） |
20（预计） |
约10 500 |
| 第十届 |
1.9（预计） |
7.4（预计） |
约. |
如图，AB是⊙O的直径，PA，PC分别与⊙O 相切于点A，C，PC交AB的延长线于点D，DE⊥PO交PO的延长线于点E。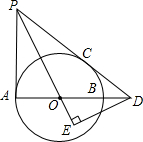
（1）求证：∠EPD=∠EDO
（2）若PC=6，tan∠PDA=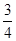
，求OE的长。