如图所示,穿过光滑水平平面中央小孔O的细线与平面上质量为m的小球P相连,手拉细线的另一端,让小球在水平面内以角速度ω1沿半径为a的圆周做匀速圆周运动。所有摩擦均不考虑。 求:
(1)这时细线上的张力多大?
(2)若突然松开手中的细线,经时间Δt再握紧细线,随后小球沿半径为b的圆周做匀速圆周运动。试问:Δt等于多大?这时的角速度ω2为多大?
将一个标有“24 V、48 W’的电灯接在电动势E="36" V,内阻r=2 Ω的直流电源下使用,今有“2Ω、50W”的定值电阻R若干只可供选用,请设计两种电路使电灯正常发光(要求使用定值电阻数最少):
(1)定值电阻与电灯串联作分压电阻使用(写出设计根据,画出电路图)
(2)定值电阻与电灯并联作分流电阻使用(写出设计根据,画出电路图)
(3)在你设计的两种电路中,哪种方法较好?说明理由。
在一个点电荷Q的电场中,Ox坐标轴与它的一条电场线重合,坐标轴上A、B两点的坐标分别为2.0m和5.0m.已知放在A、B两点的试探电荷受到的电场力方向都跟x轴的正方向相同,电场力的大小跟试探电荷所带电荷量大小的关系如图中直线A、B所示,放在A点的电荷带正电,放在B点的电荷带负电.求:
(1)B点的电场强度的大小和方向;
(2)试判断点电荷Q的电性,并确定点电荷Q的位置坐标.
如图所示,在倾角为θ的光滑固定斜面上,劲度系数分别为k1、k2的两个轻弹簧平行于斜面悬挂着,k1在上, k2在下,两弹簧之间有一质量为m1的重物,k2下端连接有一质量为m2的重物。现用力F(未知)沿斜面向上缓慢推动m2,当弹簧k1变成原长时,求: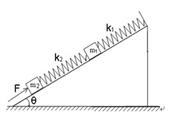
(1)k2轻弹簧的形变量;
(2)推力F的大小;
(3)m2沿斜面上移的距离。
如图所示,质量为mB=14kg的木板B放在水平地面上,质量为mA=10kg的木箱A放在木板B上。一根轻绳一端拴在木箱上,另一端拴在地面的木桩上,绳绷紧时与水 平面的夹角为θ=37°。已知木箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4。重力加速
平面的夹角为θ=37°。已知木箱A与木板B之间的动摩擦因数μ1=0.5,木板B与地面之间的动摩擦因数μ2=0.4。重力加速 度g取10m/s2。现用水平力F将木板B从木箱A下面匀速抽出,试求:(sin37°=0.6,cos37°=0.8)
度g取10m/s2。现用水平力F将木板B从木箱A下面匀速抽出,试求:(sin37°=0.6,cos37°=0.8)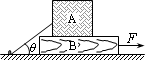
(1)绳上张力T的大小;
(2)拉力F的大小。
货车正在以v1=10m/s的速度在平直的公路上前进,货车司机突然发现在其正后方S0=25米处有一辆小车以v2=20m/s的速度做同方向的匀速直线运动,货车司机为了不让小车追上,立即加大油门做匀加速运动。
求:(1)若货车的加速度大小为a=4m/s2,小车能否追上货车?若追得上,则经多长时间追上?若追不上,小车与货车相距的最近距离为多少?
(2)若要保证小车追上货车,则货车的加速度应满足什么条件?