.在二项式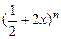 的展开式中,(Ⅰ)若第5项
的展开式中,(Ⅰ)若第5项 ,第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项;(Ⅱ)若前三项的二项式系数和等于79,求展开式中系数最大的项。
,第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项;(Ⅱ)若前三项的二项式系数和等于79,求展开式中系数最大的项。
如图,在矩形ABCD中,已知AD=2,AB=
 ,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。
,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。
在数列 中,其中
中,其中
⑴求数列 的通项公式;
的通项公式;
⑵设 ,证明:当
,证明:当 时,
时, .
.
已知函数 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(1)求a的值; (2)若 上恒成立,求
上恒成立,求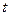 的取值范围;
的取值范围;
(3)讨论关于 的根的个数.
的根的个数.
设函数

 .对于正项数列
.对于正项数列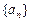 ,其前
,其前
(1)求实数 (2)求数列
(2)求数列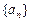 的通项公式
的通项公式
(3)若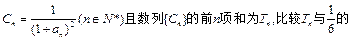 大小,并说明理由。
大小,并说明理由。
设函数 定义域为
定义域为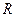 ,当
,当 时,
时, ,且对于任意的
,且对于任意的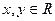 ,都有
,都有
(1)求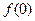 的值,并证明函数
的值,并证明函数 在
在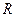 上是减函数;
上是减函数;
(2)记△ABC的三内角A、B、C的对应边分别为a,b,c,若 时,不等式
时,不等式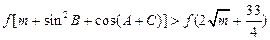 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。