给定两个命题, P: 对任意实数
对任意实数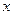 都有
都有 恒成立;Q:关于
恒成立;Q:关于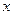 的方程
的方程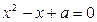 有实数根.如果P∨Q为真命题,P∧Q为假命题,求实数
有实数根.如果P∨Q为真命题,P∧Q为假命题,求实数 的取值范围.
的取值范围.
已知数列{an}的前n项Sn=pn+q(p≠0,p≠1),求数列{an}是等比数列的充要条件.
抛物线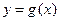 经过点
经过点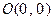 、
、 与点
与点 ,其中
,其中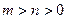 ,
,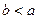 ,设函数
,设函数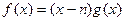 在
在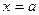 和
和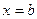 处取到极值。
处取到极值。
(1)用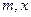 表示
表示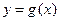 ;
;
(2)比较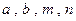 的大小(要求按从小到大排列);
的大小(要求按从小到大排列);
(3)若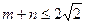 ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线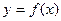 均相切,求
均相切,求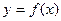 。
。
椭圆的对称中心在坐标原点,一个顶点为 ,右焦点
,右焦点 与点
与点 的距离为
的距离为 。
。
(1)求椭圆的方程;
(2)是否存在斜率 的直线
的直线 :
: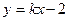 ,使直线
,使直线 与椭圆相交于不同的两点
与椭圆相交于不同的两点 满足
满足 ,若存在,求直线
,若存在,求直线 的倾斜角
的倾斜角 ;若不存在,说明理由。
;若不存在,说明理由。
已知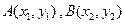 是
是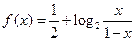 的图象上任意两点,设点
的图象上任意两点,设点 ,且
,且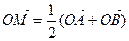 ,若
,若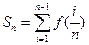 ,其中
,其中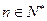 ,且
,且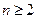 。
。
(1)求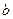 的值;
的值;
(2)求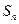 ;
;
(3)数列 中
中 ,当
,当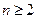 时,
时,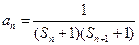 ,设数列
,设数列 的前
的前 项和为
项和为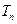 ,
,
求 的取值范围使
的取值范围使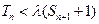 对一切
对一切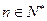 都成立。
都成立。
函数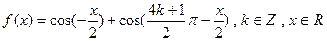 。
。
(1)求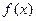 的周期;(2)解析式及
的周期;(2)解析式及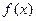 在
在 上的减区间;
上的减区间;
(3)若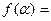
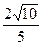 ,
,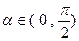 ,求
,求 的值。
的值。