(1) 个人坐在一排
个人坐在一排 个座位上,问①空位不相邻的坐法有多少种?②
个座位上,问①空位不相邻的坐法有多少种?② 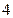 个空位只有
个空位只有 个相邻的坐法有多少种
个相邻的坐法有多少种 ?
?
(2)  的展开式奇数项的二项式系数之和为
的展开式奇数项的二项式系数之和为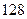 ,则求展开式中二项式系数最大项。
,则求展开式中二项式系数最大项。
在等比数列
中,
.
(1)求
;
(2)设
,求数列
的前
项和
.
已知抛物线
的焦点为
,直线
与
轴的交点为
,与
的交点为
,且
.
(1)求抛物线
的方程;
(2)过F的直线
与
相交于
两点,若
的垂直平分线
与
相交于
两点,且
四点在同一个圆上,求直线
的方程.
函数
.
(1)讨论函数
的单调性;
(2)若函数
在区间(1,2)是增函数,求
的取值范围.
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6,0.5,0.5,0.4,各人是否使用设备相互独立,
(1)求同一工作日至少3人需使用设备的概率;
(2)实验室计划购买
台设备供甲、乙、丙、丁使用,若要求"同一工作日需使用设备的人数大于
的概率小于0.1,求
的最小值.
如图,三棱柱 中,点 在平面 内的射影 在 上, , ,
(1)证明:
(2)设直线 与平面 的距离为 ,求二面角 的大小.
