为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目,对甲、乙两名运动员进行培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次,得出茎叶图如图所示.
| |
甲 |
|
乙 |
|
|
| 9 |
8 |
7 |
5 |
|
|
| 4 |
1 |
8 |
0 |
3 |
5 |
| 5 |
3 |
9 |
2 |
5 |
|
(1)从平均成绩 及发挥稳定性的角度考虑,你认为选派哪名运动员合适?
及发挥稳定性的角度考虑,你认为选派哪名运动员合适?
(2)若将频率视为概率,对甲运动员在今后的3次比赛成绩进行预测,记这3次成绩中高于80分的次数为ξ,求ξ的分布列及数学期望E(ξ)
已知圆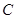 的圆心
的圆心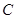 与点
与点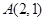 关于直线
关于直线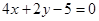 对称,圆
对称,圆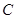 与直线
与直线 相切.
相切.
(1)设 为圆
为圆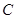 上的一个动点,若点
上的一个动点,若点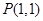 ,
,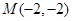 ,求
,求 的最小值;
的最小值;
(2)过点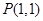 作两条相异直线分别与圆
作两条相异直线分别与圆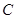 相交于
相交于 ,且直线
,且直线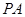 和直线
和直线 的倾斜角互补,
的倾斜角互补, 为坐标原点,试判断直线
为坐标原点,试判断直线 和
和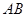 是否平行?请说明理由.
是否平行?请说明理由.
设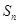 是数列
是数列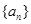 的前
的前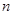 项和,
项和,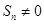 ,
,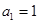 ,
,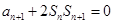 .
.
(1)求证:数列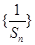 是等差数列,并
是等差数列,并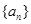 的通项;
的通项;
(2)设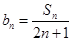 ,求数列
,求数列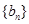 的前
的前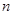 项和
项和 .
.
函数 是定义在
是定义在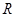 上的偶函数,
上的偶函数,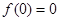 ,当
,当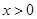 时,
时,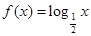 .
.
(1)求函数 的解析式;
的解析式;
(2)解不等式 ;
;
如图,已知正三棱柱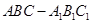 中,
中,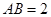 ,
, ,
,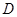 为
为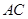 上的动点.
上的动点.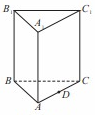
(1)求五面体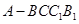 的体积;
的体积;
(2)当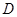 在何处时,
在何处时,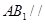 平面
平面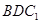 ,请说明理由;
,请说明理由;
(3)当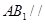 平面
平面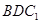 时,求证:平面
时,求证:平面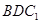
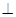 平面
平面 .
.
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如下:
得到频率分步表如下:
(1)求表中 的值,并估计这次考试全校学生数学成绩及格率(分数在
的值,并估计这次考试全校学生数学成绩及格率(分数在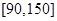 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.