某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如下:
得到频率分步表如下:
(1)求表中 的值,并估计这次考试全校学生数学成绩及格率(分数在
的值,并估计这次考试全校学生数学成绩及格率(分数在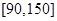 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
已知数列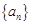 的前
的前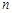 项和为
项和为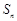 ,
,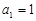 ,
, 是
是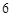 与
与 的等差中项(
的等差中项(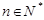 ).
).
(1)求数列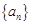 的通项公式;
的通项公式;
(2)是否存在正整数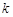 ,使不等式
,使不等式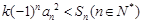 恒成立,若存在,求出
恒成立,若存在,求出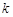
的最大值;若不存在,请说明理由.
在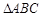 中,角
中,角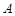 、
、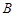 、
、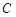 所对的边分别为
所对的边分别为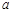 、
、 、
、 ,满足
,满足 .
.
(1)求角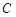 ;
;
(2)求 的取值范围.
的取值范围.
已知函数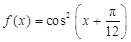 ,
,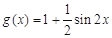 .
.
(1)设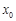 是函数
是函数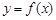 的一个零点,求
的一个零点,求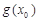 的值;
的值;
(2)求函数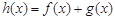 的单调递增区间.
的单调递增区间.
等差数列 中,
中,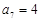 ,
,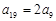 .
.
(1)求 的通项公式;
的通项公式;
(2)设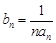 ,求数列
,求数列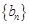 的前
的前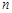 项和
项和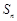 .
.
某种平面分形图如下图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为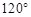 ;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来
;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来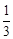 的线段,且这两条线段与原线段两两夹角为
的线段,且这两条线段与原线段两两夹角为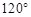 ;依此规律得到
;依此规律得到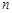 级分形图.
级分形图.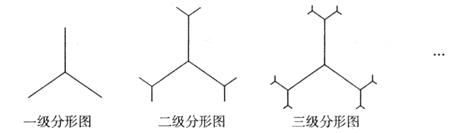
(1)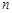 级分形图中共有条线段;
级分形图中共有条线段;
(2)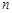 级分形图中所有线段长度之和为.
级分形图中所有线段长度之和为.