一个房间有3扇同样的窗子,其中只有一扇窗子是打开的。有一只鸟自开着的窗子飞入这个房间,它只能从开着的窗子飞出去。鸟在房子里一次又一次地向着窗户飞去,试图飞出房间. 鸟飞向各扇窗子是随机的.
(1)假定鸟是没有记忆的,若这只鸟恰好在第x次试飞时飞出了房间,求试飞次数x的分布列;
(2)假定这只鸟是有记忆的,它飞向任一窗子的尝试不多于一次,若这只鸟恰好在第y次试飞时飞出了房间,求试飞次数y的分布列;
.如图,在平面直角坐标系 中,
中,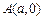
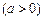 ,
,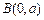 ,
,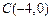 ,
,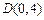 ,设
,设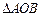 的外接圆圆心为E.
的外接圆圆心为E.
 (1)若⊙E与直线CD相切,求实数a的值;
(1)若⊙E与直线CD相切,求实数a的值; (2)设点
(2)设点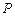 在圆
在圆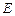 上,使
上,使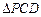 的面积等于12的点
的面积等于12的点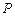 有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
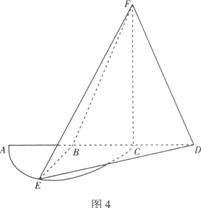
如图4,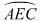 是半径为
是半径为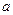 的半
的半 圆,
圆,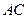 为直径,点
为直径,点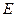 为
为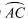 的中点,点
的中点,点 和点
和点 为线段
为线段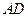 的三等分点,平面
的三等分点,平面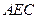 外一点
外一点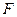 满足
满足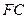
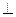 平面
平面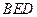 ,
,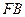 =
=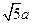 .
. 
(1)证明: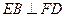 ;
;
(2)求点 到平面
到平面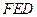 的距离.
的距离.
投掷一个质地均匀的、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面出的数字分别作为点P的横坐标和纵坐标。
(1)求点P落在区域C: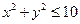 内的概率;
内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率。
某校从高一年级期末考试的学生中抽出 名学生,其成绩(均为整数)的频率分布直方图如图所示:
名学生,其成绩(均为整数)的频率分布直方图如图所示:
(Ⅰ)估计这次考试的及格率( 分及以上为及格);
分及以上为及格);
(Ⅱ)估计这次考试的平均分.
.
