已知函数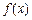 的图象在
的图象在 上连续不断,定义:
上连续不断,定义: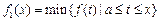
 ,
,
 .其中,
.其中,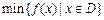 表示函数
表示函数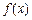 在
在 上的最小值,
上的最小值, 表示函数
表示函数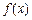 在
在 上的最大值.若存在最小正
上的最大值.若存在最小正 整数
整数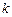 ,使得
,使得 对任意的
对任意的 成立,则称函数
成立,则称函数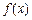 为
为 上的“
上的“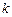 阶收缩函数”.
阶收缩函数”.
(1)已知函数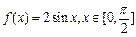 ,试写出
,试写出 ,
, 的表达式,并判断
的表达式,并判断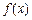 是否为
是否为 上的“
上的“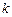 阶收缩函数”,如果是,请求对应的
阶收缩函数”,如果是,请求对应的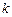 的值;如果不是,请说明理由;
的值;如果不是,请说明理由;
(2)已知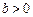 ,函数
,函数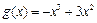 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求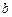 的取值范围.
的取值范围.
如图,在四棱锥P ABCD中,侧面PAD⊥底面ABCD,侧棱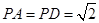 ,
, ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 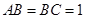 ,O为AD中点.
,O为AD中点.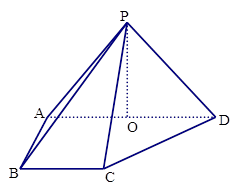
(1)求直线 与平面
与平面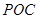 所成角的余弦值;
所成角的余弦值;
(2)求 点到平面
点到平面 的距离;
的距离;
(3)线段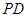 上是否存在一点
上是否存在一点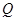 ,使得二面角
,使得二面角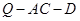 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图所示,正三棱柱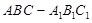 的底面边长与侧棱长均为
的底面边长与侧棱长均为 ,
, 为
为 中点.
中点.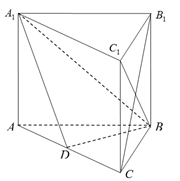
(1)求证: ∥平面
∥平面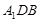 ;
;
(2)求直线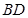 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.
直线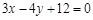 与坐标轴的交点是圆
与坐标轴的交点是圆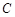 一条直径的两端点.
一条直径的两端点.
(1)求圆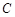 的方程;
的方程;
(2)圆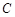 的弦
的弦 长度为
长度为 且过点
且过点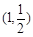 ,求弦
,求弦 所在直线的方程.
所在直线的方程.
已知直三棱柱 的所有棱长都相等,且
的所有棱长都相等,且 分别为
分别为 的中点.
的中点.
(1)求证:平面 平面
平面 ;
;
(2)求证:平面C 平面
平面 .
.
已知数列{an}的前三项与数列{bn}的前三项相同,且a1+2a2+22a3+…+2n-1an=8n对任意n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得(bk-ak)∈(0,1)?请说明理由.