如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，点F在CE上，且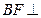
平面ACE。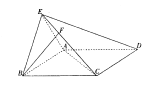
（I）求证：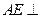
平面BCE；
（II）求二面角B—AC—E的正弦值；
（III）求点D到平面ACE的距离。
如图，平行四边形
（
按逆时针顺序排列），
边所在直线的方程分别是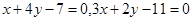
，且对角线
和
的交点为
（1）求点
的坐标
（2）求
边所在直线的方程
如图，正方体
的棱长为2，E,F,G分别是
,
的中点．
（1）求证：FG//平面
;
（2）求FG与平面
所成的角的正切值．
已知数列
及
，
，
．
（Ⅰ）求
的值，并求数列的通项公式；
（Ⅱ）设
，求数列
的前
项和
；
（Ⅲ）若
对一切正整数恒成立，求实数
的取值范围．
某房地产开发商投资810万元建一座写字楼，第一年装修费为10万元，以后每年增加20万元，把写字楼出租，每年收入租金300万元．
（Ⅰ）若扣除投资和各种装修费，则从第几年开始获取纯利润？
（Ⅱ）若干年后开发商为了投资其他项目，有两种处理方案：
①纯利润总和最大时，以100万元出售该楼；
②年平均利润最大时以460万元出售该楼，问哪种方案盈利更多？
已知函数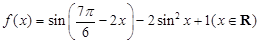
，
（Ⅰ）求函数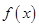
的最小正周期及单调递增区间；
（Ⅱ）在
中，三内角
，
，
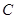的对边分别为
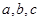，已知函数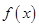的图象经过点
，
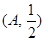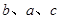成等差数列，且
，求
的值．