某房地产开发商投资810万元建一座写字楼,第一年装修费为10万元,以后每年增加20万元,把写字楼出租,每年收入租金300万元.
(Ⅰ)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(Ⅱ)若干年后开发商为了投资其他项目,有两种处理方案:
①纯利润总和最大时,以100万元出售该楼;
②年平均利润最大时以460万元出售该楼,问哪种方案盈利更多?
已知函数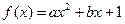 (
( ∈R且
∈R且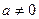 ),
), .
.
(Ⅰ)若 ,且函数
,且函数 的值域为[0, +
的值域为[0, +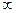 ),求
),求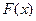 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2 , 2 ]时, 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(Ⅲ)设 ,
,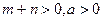 , 且
, 且 是偶函数,判断
是偶函数,判断 能否大于零?
能否大于零?
(满分16分)
某医药研究所开发一种新药,据检测,如果成人按规定的剂量服用,服药后每毫升血液中的含药量为 (微克)与服药后的时间
(微克)与服药后的时间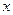 (小时)之间近似满足如图所示的曲线,其中OA 是线段,曲线 ABC 是函数
(小时)之间近似满足如图所示的曲线,其中OA 是线段,曲线 ABC 是函数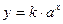 (
(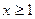 )的图象,且
)的图象,且 是常数.
是常数.
(1)写出服药后y与x的函数关系式;
(2)据测定:每毫升血液中含药量不少于2 微克时治疗疾病有效.若某病人第一次服药时间为早上 6 : 00 ,为了保持疗效,第二次服药最迟应该在当天的几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药3个小时后,该病人每毫升血液中含药量为多少微克。(结果用根号表示)
已知函数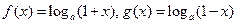 其中
其中 ,
,
设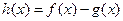 .
.
(1)求函数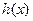 的定义域,判断
的定义域,判断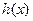 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若 ,求使
,求使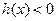 成立的
成立的 的集合
的集合
函数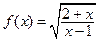 的定义域为集合A,关于x的不等式
的定义域为集合A,关于x的不等式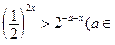 R)的解集为B,求使
R)的解集为B,求使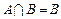 的实数a取值范围
的实数a取值范围
设 =3,计算:(1)
=3,计算:(1)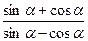 ;
;
(2)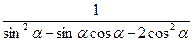 。
。