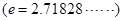设数列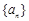 是等比数列,
是等比数列, ,公比
,公比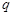 是
是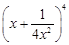 的展开式中的第二项(按x的降幂排列).
的展开式中的第二项(按x的降幂排列).
(1)用 表示通项
表示通项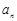 与前n项和
与前n项和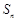 ;
;
(2)若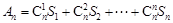 ,用
,用 表示
表示 .
.
已知:四棱锥P—ABCD的底面为直角梯形,且AB∥CD,∠DAB=90o,DC=2AD=2AB,侧面PAD与底面垂直,PA=PD,点M为侧棱PC上一点.
(1)若PA=AD,求PB与平面PAD的所成角大小;
(2)问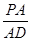 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?
已知圆锥曲线C: ,点
,点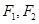 分别为圆锥曲线C的左、右焦点,点B为圆锥曲线C的上顶点,求经过点
分别为圆锥曲线C的左、右焦点,点B为圆锥曲线C的上顶点,求经过点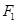 且垂直于直线
且垂直于直线 的直线
的直线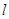 的方程.
的方程.
一个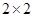 的矩阵
的矩阵 有两个特征值:
有两个特征值: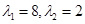 ,它们对应的一个特征向量分别为:
,它们对应的一个特征向量分别为: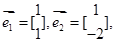 求矩阵M.
求矩阵M.
设函数 .
.
(1)若函数 图像上的点到直线
图像上的点到直线 距离的最小值为
距离的最小值为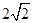 ,求
,求 的值;
的值;
(2)关于 的不等式
的不等式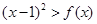 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数 的取值范围;
的取值范围;
(3)对于函数 定义域上的任意实数
定义域上的任意实数 ,若存在常数
,若存在常数 ,使得
,使得 和
和 都成立,则称直线
都成立,则称直线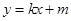 为函数
为函数 的
的
“分界线”.设 ,试探究
,试探究 是否存在“分界线”?若存在,求出“分界线”的方程,若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程,若不存在,请说明理由.