如图所示,正方形网格中,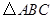 为格点三角形(即三角形的顶点都在格点上).
为格点三角形(即三角形的顶点都在格点上).
(1)把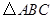 沿
沿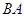 方向平移后,点
方向平移后,点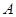 移到点
移到点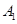 ,在网格中画出平移后得到的
,在网格中画出平移后得到的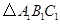 ;
;
(2)把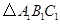 绕点
绕点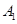 按逆时针方向旋转
按逆时针方向旋转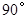 ,在网格中画出旋转后的
,在网格中画出旋转后的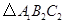 ;
;
(3)如果网格中小正方形的边长为1,求点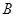 经过(1)、(2)变换的路径总长.
经过(1)、(2)变换的路径总长.
如图, 中, , 垂直平分 ,交线段 于点 (点 与点 不重合),点 为 上一点,点 为 上一点(点 与点 不重合),且 .
(1)如图1,当 时,线段 和 的数量关系是 .
(2)如图2,当 时,猜想线段 和 的数量关系,并加以证明.
(3)若 , , ,请直接写出 的长.

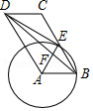
如图,在 中, ,以点 为圆心、 的长为半径的 恰好经过 的中点 ,连接 , , , 与 交于点 .
(1)求证: 与 相切.
(2)若 ,求 的长.
小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为 (元 ,日销量为 (件 ,日销售利润为 (元 .
(1)求 与 的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润 (元 与销售单价 (元 的函数关系式,当 为何值时,日销售利润最大,并求出最大利润.
如图,聪聪想在自己家的窗口 处测量对面建筑物 的高度,他首先量出窗口 到地面的距离 为 ,又测得从 处看建筑物底部 的俯角 为 ,看建筑物顶部 的仰角 为 ,且 , 都与地面垂直,点 , , , 在同一平面内.
(1)求 与 之间的距离(结果保留根号).
(2)求建筑物 的高度(结果精确到 .
(参考数据: , , ,

某超市用1200元购进一批甲玩具,用800元购进一批乙玩具,所购甲玩具件数是乙玩具件数的 ,已知甲玩具的进货单价比乙玩具的进货单价多1元.
(1)求:甲、乙玩具的进货单价各是多少元?
(2)玩具售完后,超市决定再次购进甲、乙玩具(甲、乙玩具的进货单价不变),购进乙玩具的件数比甲玩具件数的2倍多60件,求:该超市用不超过2100元最多可以采购甲玩具多少件?