(本小题满分14分)
已知椭圆 的两焦点为
的两焦点为 ,
, ,并且经过点
,并且经过点 .
.
(1)求椭圆 的方程;
的方程;
(2)已知圆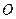 :
: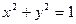 ,直线
,直线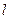 :
: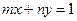 ,证明当点
,证明当点 在椭圆
在椭圆 上运动时,直线
上运动时,直线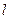 与圆
与圆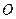 恒相交;并求直线
恒相交;并求直线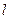 被圆
被圆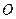 所截得的弦长的取值范围.
所截得的弦长的取值范围.
从4名男生,3名女生中选出三名代表。
(1)不同的选法共有多少种?
(2)至少有一名女生的不同的选法共有多少种?
(3)代表中男、女生都要有的不同的选法共有多少种?
在△ABC中,内角A、B、C所对边的边长分别是a、b、c,已知c=2,C=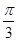 .
.
(Ⅰ)若△ABC的面积等于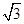 ,求a、b;
,求a、b;
(Ⅱ)若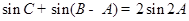 ,求△ABC的面积.
,求△ABC的面积.
已知函数f(x)=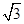 sin(ωx+φ) (0<φ<π,ω>0)过点
sin(ωx+φ) (0<φ<π,ω>0)过点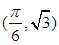 ,函数y=f(x)图象的两相邻对称轴间的距离为
,函数y=f(x)图象的两相邻对称轴间的距离为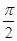 .
.
(1) 求f(x)的解析式;
(2) f(x)的图象向右平移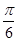 个单位后,得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
个单位后,得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积。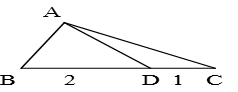
若函数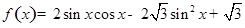
(Ⅰ)求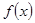 的最小正周期;
的最小正周期;
(Ⅱ)当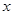
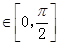 时,求函数
时,求函数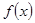 的最大值与最小值.
的最大值与最小值.