某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况，一天，他们分别在A、B 、C三个出口处，对离开园区的游客进行调查，其中
在A出口调查所得的数据整理后绘成图。
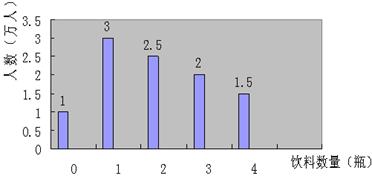
| 出口 |
B |
C |
| 人均购买饮料数量（瓶） |
3 |
2 |
（1）在A出口的被调查游客中，购买2瓶以上饮料的游客人数占A出口的被调查游客人数的____________%
（2）试问A出口的被调查游客在园区内人均购买了多少瓶饮料？
（3）已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如上表所示，若C出口的被调查人数比B出口的被调查人数多2万，且B、C两个出口的被调查游客在园区内共购买了49万瓶饮料，试问B出口的被调查游客人数为多少万？
已知关于x的方程（k﹣1）x2﹣（k﹣1）x+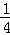
=0有两个相等的实数根，求k的值．
在△AEC和△DFB中，已知∠E=∠F，点A，B，C，D在同一直线上，并写下三个关系式：①AE∥DF，②AB=CD，③CE=BF．小明选取了关系式①，②作为条件，关系式③作为结论。你认为按照小明的选法得到的命题是真命题吗？如果是，请写出证明过程，如果不是，请举出反例．
计算
（1）解不等式组：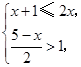
．
（2）解方程组：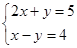
计算
（1）计算：
．
（2）解方程：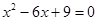
探究：如图①，△ABC是等腰直角三角形，∠ACB=90°，AC=BC．点D在边AB上（D不与A，B重合），连结CD，过点C作CE⊥CD，且CE=CD，连结DE、AE．
求证：△BCD≌△ACE．
应用：如图②，在图①的基础上，点D在BA的延长线上，其他条件不变．若AD=
AB，AB=4，求DE的长．