．（本小题满分12分）
某地区对12岁儿童瞬时记忆能力进行调查．瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人，下表为该班学生瞬时记忆能力的调查结果．例如表中听觉记忆能力为中等，且视觉记忆能力偏高的学生为3人．
 视觉 |
视觉记忆能力 |
||||
| 偏低 |
中等 |
偏高 |
超常 |
||
| 听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
| 中等 |
1 |
8 |
3 |
 |
|
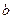| 偏高 |
2 |
 |
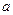0 |
1 |
|
| 超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失，只知道从这40位学生中随机抽取一个，视觉记忆能力恰为中等，且听觉记忆能力为中等或中等以上的概率为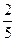
．
（1）试确定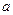、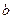的值；
（2）从40人中任意抽取3人，求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率；
（3）从40人中任意抽取3人，设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为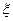
，求随机变量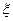的数学期望
．
（本小题满分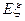7分）选修4-2：矩阵与变换
二阶矩阵
；
（Ⅰ）求点
在变换
作用下得到的点
；
（Ⅱ）设直线
在变换作用下得到了直线
，求点
到直线的距离．
（本小题满分14分）已知函数
（
且
），
．
（Ⅰ）若
在定义域上有极值，求实数
的取值范围；
（Ⅱ）当
时，若对
，总
，使得
，求实数
的取值范围；（其中
为自然对数的底数）；
（Ⅲ）对
，且
，证明：
．
（本小题满分13分）设椭圆
的左、右焦点分别为
，上顶点为
，在
轴负半轴上有一点
，满足
， 
，且
是过、、
三点的圆上的点，到直线
的最大距离等于椭圆长轴的长，求椭圆
的方程；
（Ⅰ）求椭圆的方程；
（Ⅱ）若过右焦点作斜率为
的直线
与椭圆交于
、
两点，线段
的中垂线与轴相交于点
，求实数
的取值范围．
（本小题满分13分）正方形
的边长为
，
分别为边
的中点，
是线段
的中点，如图，把正方形沿折起，设
．
（Ⅰ）求证：无论
取何值，
与
不可能垂直；
（Ⅱ）设二面角
的大小为
，当
时，求
的值．
（本小题满分13分）某销售公司对其员工进行年终考核，在本次考核中只有合格和优秀两个等次，若考核为合格，则奖励奖金1万元；考核为优秀，奖励奖金2万元，假设甲、乙、丙三个分店考核为优秀的概率分别为
、、
，他们考核所得的等次相互独立．
（Ⅰ）求在这次考核中，甲、乙、丙三个员工中至少有一名考核为优秀的概率；
（Ⅱ）记在这次考核中甲、乙、丙三个员工所得的奖金之和为随机变量
，求随机变量的分布列和数学期望
。