(本小题满分14分)
已知双曲线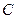 :
: 和圆
和圆 :
: (其中原点
(其中原点 为圆心),过双曲线
为圆心),过双曲线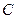 上一点
上一点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 、
、 .
.
(1)若双曲线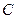 上存在点
上存在点 ,使得
,使得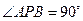 ,求双曲线离心率
,求双曲线离心率 的取值范围;
的取值范围;
(2)求直线 的方程;
的方程;
(3)求三角形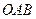 面积的最大值.
面积的最大值.
设集合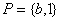 ,
,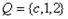 ,
,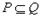 , 若
, 若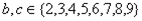 .
.
(1)求b = c的概率;
(2)求方程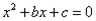 有实根的概率
有实根的概率
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.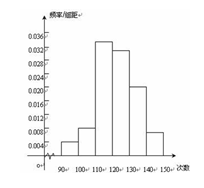
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
(3)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由。
已知数列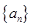 的前
的前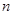 项和为
项和为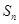 ,点
,点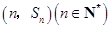 均在二次函数
均在二次函数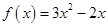 的图象上.
的图象上.
(1)求数列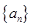 的通项公式;
的通项公式;
(2)设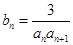 ,求数列
,求数列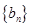 的前
的前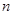 项和
项和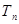
已知函数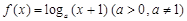 在区间[1,7]上的最大值比最小值大
在区间[1,7]上的最大值比最小值大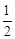 ,求a的值
,求a的值
已知集合P={x|x2-x-2>0},Q={x|x2+4x+a<0},若P⊇Q,求实数a的取值范围.