求出函数 的单调递增区间.
的单调递增区间.
如图, 垂直于矩形
垂直于矩形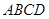 所在的平面,
所在的平面,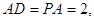

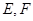 分别是
分别是 、
、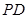 的中点.
的中点.
(Ⅰ)求证: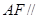 平面
平面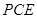 ;
;
(Ⅱ)求证:平面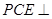 平面
平面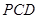 ;
;
(Ⅲ)求二面角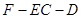 的大小.
的大小.
在两个袋内,分别装有编号为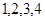 四个数字的
四个数字的 张卡片,现从每个袋内任取一张卡片.
张卡片,现从每个袋内任取一张卡片.
(Ⅰ)利用卡片上的编号写出所有可能抽取的结果;
(Ⅱ)求取出的卡片上的编号之和不大于 的概率;
的概率;
(Ⅲ)若第一个袋内取出的卡片上的编号记为 ,第二个袋内取出的卡片上的编号记为
,第二个袋内取出的卡片上的编号记为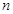 ,求
,求 的概率.
的概率.
已知函数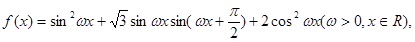 在
在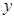 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为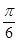 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若将函数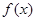 的图象向右平移
的图象向右平移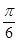 个单位后,再将得到的图象上各点横坐标伸长到原来的
个单位后,再将得到的图象上各点横坐标伸长到原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数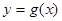 的图象,求函数
的图象,求函数 的最大值及单调递减区间.
的最大值及单调递减区间.
(12分) 对于在区间 [ m,n ] 上有意义的两个函数 与
与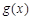 ,如果对任意
,如果对任意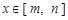 ,均有
,均有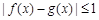 ,则称
,则称 与
与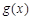 在 [ m,n ] 上是友好的,否则称
在 [ m,n ] 上是友好的,否则称 与
与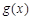 在 [ m,n ]是不友好的.现有两个函数
在 [ m,n ]是不友好的.现有两个函数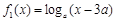 与
与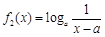 (a > 0且
(a > 0且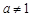 ),给定区间
),给定区间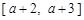 .
.
(1)与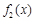 在给定区间
在给定区间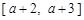 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;
(2)与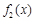 在给定区间
在给定区间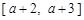 上是否友好.
上是否友好.
(12分) 已知a > 0,函数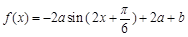 ,当
,当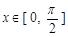 时,
时, .
.
(1)求常数a、b的值;
(2)设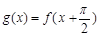 且
且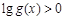 ,求
,求 的单增区间.
的单增区间.