已知函数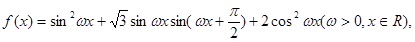 在
在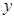 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为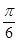 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若将函数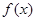 的图象向右平移
的图象向右平移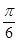 个单位后,再将得到的图象上各点横坐标伸长到原来的
个单位后,再将得到的图象上各点横坐标伸长到原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数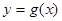 的图象,求函数
的图象,求函数 的最大值及单调递减区间.
的最大值及单调递减区间.
有关专家建议,在未来几年内,中国的通货膨胀率保持在3%左右,这将对我国经济的稳定有利无害.所谓通货膨胀率为3%,指的是每年消费品的价格增长率为3%.在这种情况下,某种品牌的钢琴2004年的价格是10 000元,请用流程图描述这种钢琴今后四年的价格变化情况,并输出四年后的价格.
写出通过尺轨作图确定线段AB的一个5等分点的程序框图.
下图所示的是一个算法的流程图,已知a1=3,输出的b=7,求a2的值. 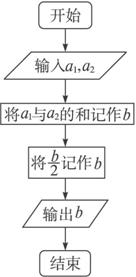
已知一个三角形三条边的边长分别为a,b,c,利用海伦—秦九韶公式设计一个计算三角形面积的算法,并画出程序框图表示.(已知三角形三边边长分别为a,b,c,则三角形的面积为S=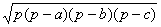 ),其中p=
),其中p=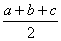 .这个公式被称为海伦—秦九韶公式)
.这个公式被称为海伦—秦九韶公式)
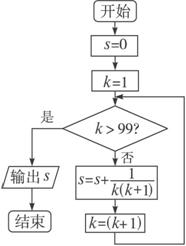
观察下面的程序框图,指出该算法解决的问题.