定义函数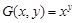 ,其中,
,其中,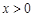 ,
, .
.
(Ⅰ)设函数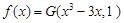 ,求
,求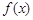 的定义域;
的定义域;
(Ⅱ)设函数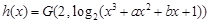 的图像为曲线
的图像为曲线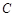 ,若存在实数
,若存在实数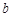 使得曲线
使得曲线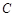 在
在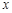
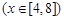 处有斜率为
处有斜率为 的切线,求实数
的切线,求实数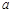 的取值范围;
的取值范围;
(Ⅲ)当 且
且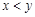 时,试比较
时,试比较 与
与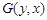 的大小(只写出结论).
的大小(只写出结论).
如果函数f(x)的定义域为{x|x>0},且f(x)为增函数,f(x·y)=f(x)+f(y).
(Ⅰ)求证: f( )=f(x) -f(y);
)=f(x) -f(y);
(Ⅱ)已知f(3)=1,且f(a)-f(a-1)>2,求a的取值范围
设二次函数 在区间
在区间 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合 .
.
(Ⅰ)若 ,且
,且 ,求M和m的值;
,求M和m的值;
(Ⅱ)若 ,且
,且 ,记
,记 ,求
,求 的最小值
的最小值
如图,在长方体 中,
中, 为
为 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)判断并证明,点 在棱
在棱 上什么位置时,平面
上什么位置时,平面 平面
平面 .
.
求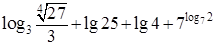 的值
的值
(本小题满分12分)
已知函数f(x)=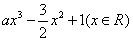 ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间 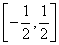 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.