（本小题满分14分）
函数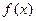
定义在区间[a, b]上，设“
”表示函数
在集合D上的最小值，“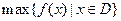
”表示函数在集合D上的最大值．现设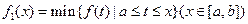
，
，
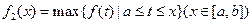若存在最小正整数k，使得
对任意的
成立，则称函数为区间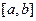
上的“第k类压缩函数”．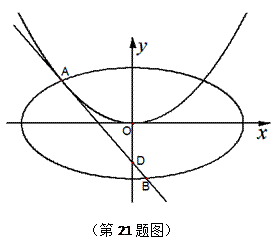
(Ⅰ) 若函数
，求的最大值，写出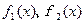
的解析式；
(Ⅱ) 若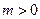
，函数
是
上的“第3类压缩函数”，求m的取值范围．
（本小题满分l2分） 已知函数f（x）=ax3+bx2－3x在x=±1处取得极值.
（1）求函数f（x）的解析式；
（2）求证：对于区间[－1，1]上任意两个自变量的值x1，x2，都有|f（x1）－f（x2）|≤4；
（3）若过点A（1，m）（m≠－2）可作曲线y=f（x）的三条切线，求实数m的取值范围.
（本小题满分12分）
平面内动点P（x，y）与两定点A（-2, 0）, B（2,0）连线的斜率之积等于
，若点P的轨迹为曲线E，过点Q
作斜率不为零的直线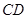
交曲线E于点
．
（1）求曲线E的方程；
（2）求证：
；
（3）求
面积的最大值．
如图，四边形ABCD中，AB⊥AD，AD∥BC，AD＝6，BC＝4，AB＝2，E、F分别在BC、AD上，EF∥AB．现将四边形ABEF沿EF折起，使得平面ABEF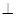
平面EFDC．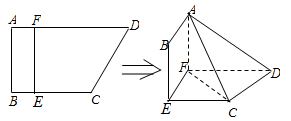
（1）当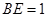
，是否在折叠后的AD上存在一点
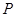，使得CP∥平面ABEF？若存在，求出P点位置，若不存在，说明理由；
（2）设BE＝x，问当x为何值时，三棱锥A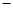
CDF的体积有最大值？并求出这个最大值．
（本小题满分12分）在
中，已知角A、B、C所对的边分别为
，直线
与直线
互相平行（其中
）.
（1）求角A的值；
（2）若
的取值范围.
（本小题满分12分）“等比数列 
中，
，且 
是 
和 
的等差中项，若 
（1）求数列 
的通项公式；
（2）求数列
的前
项和.