已知数列{an}和{bn}满足:a1=λ,an+1= an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
(1)对任意实数λ,证明:数列{an}不是等比数列;
(2)试判断数列{bn}是否为等比数列,并证明你的结论.
(本小题满分13分)坐标系 中,已知椭圆
中,已知椭圆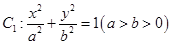 的其中一个顶点坐标为B(0,1),且点
的其中一个顶点坐标为B(0,1),且点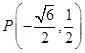 在
在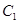 上.
上.
(Ⅰ)求椭圆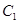 的方程;
的方程;
(Ⅱ)若直线 与椭圆
与椭圆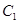 交于M,N且
交于M,N且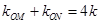 ,求证:
,求证: 为定值.
为定值.
(本小题满分12分)已知公差不为零的等差数列 ,满足
,满足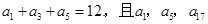 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,数列
,数列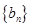 的前n项和为
的前n项和为 ,求证:
,求证: .
.
(本小题满分12分)已知四棱锥 中,底面ABCD为直角梯形,BC//AD,
中,底面ABCD为直角梯形,BC//AD, ,且PA=AB=BC=1,AD=2,
,且PA=AB=BC=1,AD=2, 平面ABCD,E为AB的中点.
平面ABCD,E为AB的中点.
(Ⅰ)证明: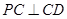 ;
;
(Ⅱ)在线段PA上是否存在一点F,使EF//平面PCD,若存在,求 的值.
的值.
(本小题满分12分)国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施,某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请求出70~80分数段的人数;
(Ⅱ)现根据测试成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、 、第五组)中任意选出两人,形成搭档小组.若选出的两人成绩差大于20,则称这两人为“搭档组”,试求选出的两人为“搭档组”的概率.
(本小题满分12分)
已知函数 .
.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)当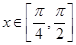 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.