(本小题满分16 分)如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
分)如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点.
(1)求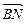 的长;
的长;
(2)求 的值;
的值;
(3)求证:A1B⊥C1M.
设函数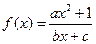 是奇函数(a,b,c都是整数),且
是奇函数(a,b,c都是整数),且
 ,
,
(1)求a,b,c的值;
(2)当x<0,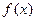 的单调性如何?用单调性定义证明你的结论。
的单调性如何?用单调性定义证明你的结论。
已知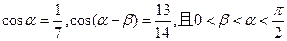 ,
,
( 1)求
1)求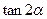 的值;
的值;
(2)求β。
已知函数 ,
,
(1)求函数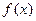 的单调区间;
的单调区间;
(2)若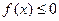 恒成立,试确定实数
恒成立,试确定实数 的取
的取 值范围;
值范围;
(3)证明: (
(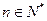 且
且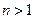 )
)
已知函数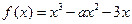 (1)若
(1)若
 在区间
在区间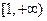 上是增函数,求实数
上是增函数,求实数 的取值范围; (2)若
的取值范围; (2)若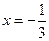 是
是 的极值点,求
的极值点,求 在
在 上的最大值;(3)在(2)的条件下,是否存在实数
上的最大值;(3)在(2)的条件下,是否存在实数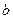 ,使得函数
,使得函数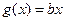 的图像与函数
的图像与函数 的图象恰有3个交点?若存在,请求出实数
的图象恰有3个交点?若存在,请求出实数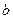 的取值范围;若不存在,试说明理由。
的取值范围;若不存在,试说明理由。
(本小题12分)设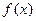 是定义在
是定义在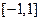 上的函数,且对任意
上的函数,且对任意 ,当
,当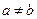 时,都有
时,都有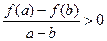 ;
;
(1)当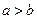 时,比较
时,比较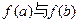 的大小;
的大小;
(2)解不等式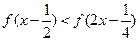 ;
;
(3)设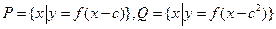 且
且 ,求
,求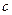 的取值范围。
的取值范围。