(本小题8分)书架上有10本不同的书,其中语文书4本,数学书3本,英语书3本,现从中取出3本书.求:
( 1 )3本书中至少有1本是数学书的概率;
( 2 ) 3本书不全是同科目书的概率.
3本书不全是同科目书的概率.
解:(1)3本书中至少有 1本是数学书的概率为
1本是数学书的概率为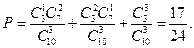
 (4分)
(4分)
或解  (4分)
(4分)
(2)事件“3本书不全是同科目书”的对立事件是事件“3本书是同科目书”,
而事件“3本书是同科目书”的概率为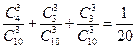 (7分
(7分
∴3本书不全是同科目书的概率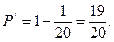
在△ABC中,A点的坐标为(3,0),BC边长为2,且BC在y轴上的区间[-3,3]上滑动.
(1)求△ABC外心的轨迹方程;
(2)设直线l∶y=3x+b与(1)的轨迹交于E,F两点,原点到直线l的距离为d,求 的最大值.并求出此时b的值
的最大值.并求出此时b的值
(本小题满分14分)
已知,椭圆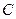 过点
过点 ,两个焦点为
,两个焦点为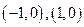 。
。
(1)求椭圆C的方程;

(2)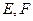 是椭圆
是椭圆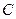 上的两个动点,如果直线
上的两个动点,如果直线 的斜率与
的斜率与 的斜率互为相反数,证明直线
的斜率互为相反数,证明直线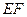 的斜率为定值,并求出这个定值。
的斜率为定值,并求出这个定值。
正方形 的一条边
的一条边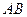 在直线
在直线 上,另外两个顶点
上,另外两个顶点 在抛物线
在抛物线 上,求正方形的边长.
上,求正方形的边长.
(本小题满分14分)现有一批货物用轮船从甲地运往乙地,甲乙两地距离为500海里,已知该船最大速度为45海里/小时,每小时运输成本由燃料费用和其它费用组成.轮船每小时的燃料费用与轮船速度的平方成正比,其余费用为每小时960元.已知轮船速度为20海里/小时,全程运输成本为30000元.
(1)把全程运输成本 (元)表示为速度
(元)表示为速度 (海里/小时)的函数;
(海里/小时)的函数;
(2)为了使全程运输成本最小,轮船应为多大速度行驶?
(本小题满分14分)如图,椭圆以边长为1的正方形ABCD的对角顶点A,C为焦点,且经过各边的中点,试建立适当的坐标系,求椭圆的方程。