( (本题满分15分
)椭圆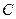
的中心在原点，焦点在
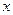轴上，离心率为
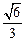，并与直线
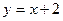相切.
(Ⅰ)求椭圆的方程；
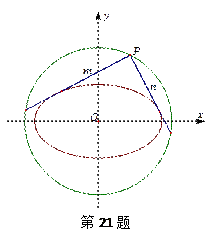
(Ⅱ)如图，过圆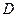
：
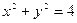上任意一点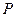
作椭圆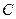的两条切线
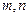． 求证：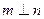
．
（本小题满分10分）选修4-4：坐标系与参数方程
在直角坐标系
中，以坐标原点
为极点，以
轴正半轴为极轴建立极坐标系．已知曲线
（
为参数），曲线
．
（Ⅰ）将曲线
化成普通方程，将曲线
化成参数方程；
（Ⅱ）判断曲线和曲线的位置关系．
（本小题满分10分）选修4-1：几何证明选讲
已知如图，
、
是
上的点，、
、
三点在一条直线上，直线
经过圆心
，
，
．
（Ⅰ）求证：直线
是的切线；
（Ⅱ）若
，
，求
的长．
（本小题满分12分）已知函数
（
），
．
（Ⅰ）求证：
在区间
上单调递增；
（Ⅱ）若
，函数
在区间上的最大值为
，求的解析式，并判断是否有最大值和最小值，请说明理由（参考数据：
）．
（本小题满分12分）已知命题
抛物线
的焦点
在椭圆
上．命题
直线
经过抛物线的焦点，且直线过椭圆的左焦点
．
是真命题．
（Ⅰ）求直线的方程；
（Ⅱ）直线与抛物线相交于
、
，直线
、
分别切抛物线于、，求、的交点
的坐标．
（本小题满分12分）已知函数
以
为切点的切线方程是
．
（Ⅰ）求实数
，
的值；
（Ⅱ）求函数
的单调区间；
（Ⅲ）求的零点个数．