(本小题满分12分)已知函数 以
以 为切点的切线方程是
为切点的切线方程是 .
.
(Ⅰ)求实数 ,
, 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)求 的零点个数.
的零点个数.
已知函数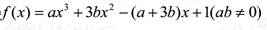 在x=1处取得极值,在x=2处的切线平行于向量
在x=1处取得极值,在x=2处的切线平行于向量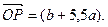
(1)求a,b的值,并求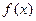 的单调区间;
的单调区间;
(2)是否存在正整数m,使得方程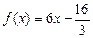 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
已知函数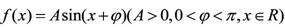 的最大值是2,
的最大值是2, 其图象经过点
其图象经过点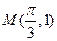 .
.
(1)求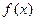 的解析式;
的解析式;
(2)已知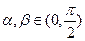 ,且
,且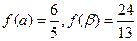 ,
,
求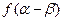 的值.
的值.
(本小题满分14分)
已知函数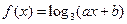 的图象经过点A(2,1)和B(5
的图象经过点A(2,1)和B(5 ,2),记
,2),记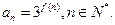
(1)求数列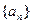 的通项公式;
的通项公式;
(2)设 ,若3-
,若3-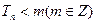 恒成立,求
恒成立,求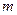 的最小值
的最小值
(本小题满分14分)
矩形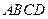 的两条对角线相交于点M(2,0),
的两条对角线相交于点M(2,0),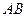 边所在直线的方程为
边所在直线的方程为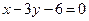 ,点T(-1,1)在
,点T(-1,1)在 边所在直线上.
边所在直线上.
(1)求 边所在直线的方程;
边所在直线的方程;
(2)求矩形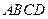 外接圆的方程;
外接圆的方程;
(3)若动圆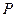 过点N(-2,0),且与矩形
过点N(-2,0),且与矩形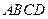 的外接圆外切,求动圆
的外接圆外切,求动圆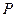 的圆心的轨迹方程.
的圆心的轨迹方程.
18.(本小题满分13分)
如图,直二面角 中,四边形
中,四边形 是边长为
是边长为
2的正方形, 为CE上的点,且
为CE上的点,且 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)求三棱锥E-ABC的体积.