(本题满分15分)
已知函数 .
.
(Ⅰ)若 无极值点,但其导函数
无极值点,但其导函数 有零点,求
有零点,求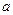 的值;
的值;
(Ⅱ)若 有两个极值点,求
有两个极值点,求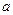 的取值范围,并证明
的取值范围,并证明 的极小值小于
的极小值小于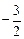 .
.
设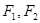 分别是椭圆的
分别是椭圆的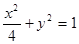 左,右焦点。
左,右焦点。
(1)若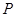 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且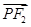 ·
·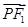 =
=
 求点
求点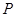 的坐标。
的坐标。
(2)设过定点 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点 ,且
,且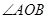 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线 的斜率
的斜率 的取值范围。
的取值范围。
已知:数列{an}的前n项和为Sn,满足Sn=2an-2n(n∈N*)
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=log2(an+2),而Tn为数列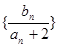 的前n项和,求Tn.
的前n项和,求Tn.
已知双曲线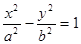 的离心率
的离心率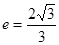 ,过
,过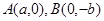 的直线到原点的距离是
的直线到原点的距离是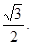
(1)求双曲线的方程;
(2)已知直线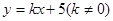 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
(本小题满分12分)如图,正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1.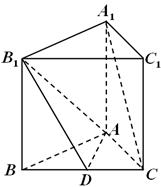
(I)求证:A1C//平面AB1D;
(II)求二面角B—AB1—D的大小;
(III)求点C到平面AB1D的距离.
已知直四棱柱ABCD—A′B′C′D′的底面是菱形, ,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.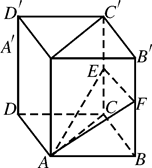
(1)求证:平面AEF⊥平面AA′C′C;
(2)求截面AEF与底面ABCD所成二面角的大小.