(本小题满分12分)
在一个盒子中,放有标号分别为1,2,3的三张卡片,先从这个盒子中有放回地先后抽取两张卡片,设这两张卡片的号码分别为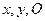 为坐标原点,
为坐标原点,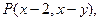 记
记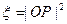
(1)求随机变量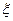 的最大值,并求事件“
的最大值,并求事件“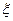 取最大值”的概率;
取最大值”的概率;
(2)求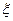 的分布
的分布 列及数学期望。
列及数学期望。
从装有6个白球、4个黑球和2个黄球的箱中随机地取出两个球,规定每取出一个黑球赢2元,而每取出一个白球输1元,取出黄球无输赢,以X表示赢得的钱数,则随机变量X可以取哪些值?求X的概率分布.
设离散型随机变量 的分布列P(
的分布列P( =
= )=ak,k=1,2,3,4,5.
)=ak,k=1,2,3,4,5.
(1)求常数a的值;
(2)求P( ≥
≥ );
);
(3)求P( <
< <
< ).
).
某校组织一次冬令营活动,有8名同学参加,其中有5名男同学,3名女同学,为了活动的需要,要从这8名同学中随机抽取3名同学去执行一项特殊任务,记其中有X名男同学.
(1)求X的概率分布;
(2)求去执行任务的同学中有男有女的概率.
设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
袋中有4个红球,3个黑球,从袋中随机地抽取4个球,设取到一个红球得2分,取到一个黑球得1分.
(1)求得分X的概率分布;
(2)求得分大于6的概率.