(本小题满分14分)如图,在一个由矩形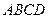 与正三角形
与正三角形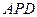 组合而成的平面图形中,
组合而成的平面图形中, 现将正三角形
现将正三角形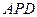 沿
沿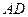 折成四棱锥
折成四棱锥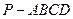 ,使
,使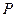 在平面
在平面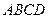 内的射影恰好在边
内的射影恰好在边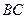 上.
上.


(1)求证:平面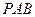 ⊥平面
⊥平面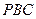 ;
;
(2)求直线 与平面
与平面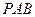 所成角的正弦值.
所成角的正弦值.
|
已知函数
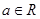
(I) 解关于 的不等式
的不等式 
(II)若函数 的图象恒在函数
的图象恒在函数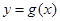 的上方,求实数
的上方,求实数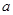 的取值范围。
的取值范围。
以直角坐标系的原点O为极点,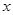 轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,
轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4, ),若直线
),若直线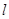 过点P,且倾斜角为
过点P,且倾斜角为 ,圆C以M为圆心,4为半径。
,圆C以M为圆心,4为半径。
(I)求直线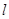 的参数方程和圆C的极坐标方程。
的参数方程和圆C的极坐标方程。
(II)试判定直线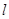 与圆C的位置关系。
与圆C的位置关系。
如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,垂是为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点。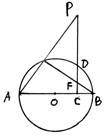
(I)求证:∠PFE=∠PAB(II)求证:CD2=CF·CP
已知函数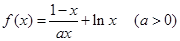
(I)当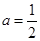 时,求
时,求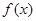 在[1,
在[1,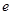 ]上的取值范围。
]上的取值范围。
(II)若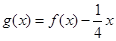 在[1,
在[1,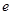 ]上为增函数,求a的取值范围。
]上为增函数,求a的取值范围。
已知平面上动点P(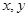 )及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为
)及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为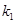 、
、 且
且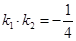
(I)求动点P所在曲线C的方程。
(II)设直线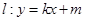 与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线
与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线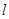 的距离。(O为坐标原点)
的距离。(O为坐标原点)