(本小题10分)
已知数列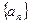 中,
中,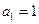
 。
。
(Ⅰ)求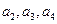 的值;
的值;
(Ⅱ)猜想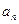 的通项公式,并用数学归纳法给予证明。
的通项公式,并用数学归纳法给予证明。
已知 ,
, .
.
(1)求 的值;
的值;
(2)当 时,求
时,求 的最值.
的最值.
设函数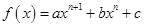
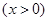 ,其中
,其中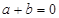 ,
, 为正整数,
为正整数,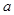 、
、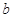 、
、 均为常数,曲线
均为常数,曲线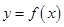 在
在 处的切线方程为
处的切线方程为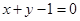 .
.
(1)求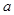 、
、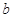 、
、 的值;
的值;
(2)求函数 的最大值;
的最大值;
(3)证明:对任意的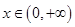 都有
都有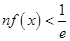 .(
.(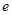 为自然对数的底)
为自然对数的底)
如图,已知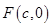 是椭圆
是椭圆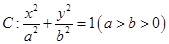 的右焦点;圆
的右焦点;圆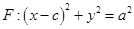 与
与 轴交于
轴交于 两点,其中
两点,其中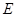 是椭圆
是椭圆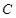 的左焦点.
的左焦点.
(1)求椭圆 的离心率;
的离心率;
(2)设圆 与
与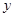 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 是点
是点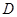 关于
关于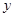 轴的对称点,试判断直线
轴的对称点,试判断直线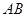 与圆
与圆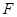 的位置关系;
的位置关系;
(3)设直线 与圆
与圆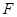 交于另一点
交于另一点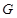 ,若
,若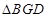 的面积为
的面积为 ,求椭圆
,求椭圆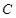 的标准方程.
的标准方程.
如图,已知 、
、 、
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且 ,
, .
.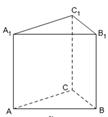
(1)求证:平面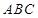 //平面
//平面 ;
;
(2)若 平面
平面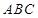 ,且
,且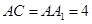 ,
, ,
,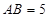 ,求证:
,求证: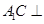 平面
平面 ;
;
(3)在(2)的条件下,设点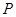 为
为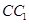 上的动点,求当
上的动点,求当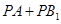 取得最小值时
取得最小值时 的长.
的长.
在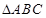 中,角
中,角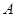 、
、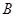 、
、 所对应的边为
所对应的边为 、
、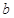 、
、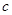 .
.
(1)若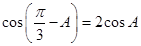 ,求
,求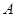 的值;
的值;
(2)若 ,且
,且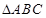 的面积
的面积 ,求
,求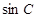 的值.
的值.