（本题满分为14分）平面直角坐标系中，正方形AOBC如图所示，点C的坐标为（a，a），其中a使得式子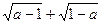
有意义，反比例函数
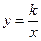的图象经过点C.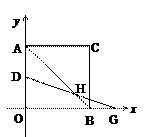
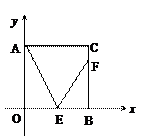
（1）求反比例函数解析式.
（2）若有一点D自A向O运动，且满足AD2=OD·AO，求此时D点坐标.
（3）若点D在AO上、G为OB的延长线上的点，AD=BG，连接AB交DG于点H，写出AB－2HB与AD之间的数量关系（直接写出不需证明）.
（4）如图，点E为正方形AOBC的OB边一点，点F为BC上一点且∠CAE=∠FEA=60°，求直线EF的解析式.
计算：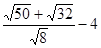
；
计算：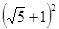
某公园门票价格，对达到一定人数的团队，按团体票优惠，现有A、B、C三个旅游团共72人，如果各团单独购票，门票依次为360元、384元、480元；如果三个团合起来购票，总共可少花72元．
⑴这三个旅游团各有多少人？
⑵在下面填写一种票价方案，使其与上述购票情况相符：
| 售 票 处 |
|
| 普通票 |
团体票(人数须_______________) |
| 每人___________元 |
每人___________元 |
尺规作图. 如图,已知
，求作：线段MN, 使其同时满足下列3个条件（要求：用尺规作图，保留作图痕迹，不写作法和结论）：
（1）点M在AC上，N在AB上；
（2）MN⊥AC
（3）AN+MN=AB。
如图，
为直角，点
为线段
的中点，点
是射线
上的一个动点（不与点
重合），连结
，作
，垂足为
，连结
，过点作
，交
于
．
（1）求证：BF=EF；
（2）当
取什么值或范围时，有AC//EF，并说明理由。