已知 AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,
求证:AB=2BC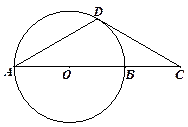
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售高订购,决定当一次订量超过100个时,每多订购一个,订购的全部零件的出厂单价降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰好降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1 000个,利润又是多少元(工厂售出一个零件的利润=实际出厂单价-成本价)?
如图,在四棱锥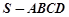 中,底面
中,底面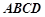 是直角梯形,
是直角梯形, ∥
∥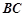 ,
, ,
,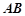 ⊥平面SAD,点
⊥平面SAD,点 是
是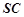 的中点,且
的中点,且 ,
,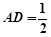 .
. 
(1)求四棱锥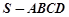 的体积;
的体积;
(2)求证: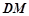 ∥平面
∥平面 ;
;
(3)求直线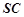 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.
在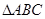 中,角
中,角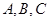 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,
,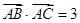 .
.
(1)求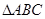 的面积;(2)若
的面积;(2)若 ,求
,求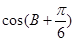 的值。
的值。
已知等差数列 的前
的前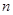 项和为
项和为 ,且
,且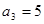 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设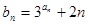 ,求数列
,求数列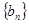 的前
的前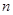 项和
项和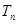 .
.
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如右图所示.
(1)下表是年龄的频数分布表,求正整数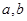 的值;
的值;
| 区间 |
[25,30) |
[30,35) |
[35,40) |
[40,45) |
[45,50] |
| 人数 |
50 |
50 |
 |
150 |
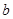 |
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.