已知数列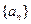 的前
的前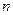 项和为
项和为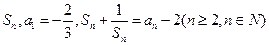
(I)求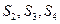 的值;
的值;
(Ⅱ)猜想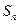 的表达式;并用数学归纳法加以证明。
的表达式;并用数学归纳法加以证明。
如图, ,
, 是两个小区的所在地,
是两个小区的所在地, ,
, 到一条公路
到一条公路 的垂直距离
的垂直距离 km,
km, km,
km, 两端之间的距离为4km.某公交公司将在
两端之间的距离为4km.某公交公司将在 之间找一点
之间找一点 ,在
,在 处建造一个公交站台.
处建造一个公交站台.
(1)设 ,试写出用
,试写出用 表示
表示 正切的函数关系式,并给出
正切的函数关系式,并给出 的范围;
的范围;
(2)能否找到一点 ,使点
,使点 到C,D两小区的距离之和(
到C,D两小区的距离之和( )最小.若能,请说明理由,并求出
)最小.若能,请说明理由,并求出 的值;若不能,也请说明理由.
的值;若不能,也请说明理由.
如图,两块直角三角板拼在一起,已知 ,
,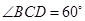 .
.
(1)若记 ,
, ,试用
,试用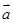 ,
, 表示向量
表示向量 、
、 ;
;
(2)若 ,求
,求
 .
.
设函数
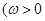 ,
, 为常数
为常数 .
.
(1)若 的图象中相邻两对称轴之间的距离不小于
的图象中相邻两对称轴之间的距离不小于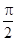 ,求
,求 的取值范围;
的取值范围;
(2)若 的最小正周期为
的最小正周期为 ,且当
,且当 时,
时, 的最大值是
的最大值是 ,又
,又 ,求
,求 的值.
的值.
已知 在同一平面内,且
在同一平面内,且 .
.
(1)若 ,且
,且 ,求
,求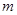 的值;
的值;
(2)若 ,且
,且 ,求向量
,求向量 与
与 的夹角.
的夹角.
一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各一个,这些球除颜色外都相同.
(1)求搅匀后从中任意摸出1个球,恰好是红球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,求至少有一次摸出的球是红球的概率.