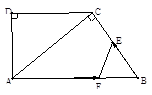我国青海省玉树地区发生强烈地震以后,国家立即启动救灾预案,积极展开向灾区运送救灾物资和对伤员的救治工作.已知西宁机场和玉树机场相距800千米,甲、乙两机沿同一航线各自从西宁、玉树出发,相向而行.如图,线段AB、CD分别表示甲、乙两机离玉树机场的距离S(百千米)和所用去的时间t(小时)之间的函数关系的图象(注:为了方便计算,将平面直角坐标系中距离S的单位定为(百千米)).观察图象回答下列问题: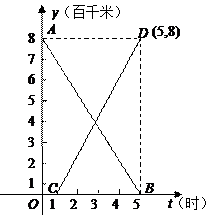
(1)乙机在甲机出发后几小时,才从玉树机场出发?甲、乙两机的飞行速度每小时各为多少千米?
(2)求甲、乙两机各自的S与 t的函数关系式;
t的函数关系式;
(3)甲、乙两机相遇时,乙机飞行了几小时?离西宁机场多少千米?
如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC.猜想:线段OD与BC有何数量和位置关系,并证明你的结论.
求证:PC是⊙O的切线

问题情境:
用同样大小的黑色棋子按如图所示的规律摆放,则第2012个图共有多少枚棋子?
建立模型:
有些规律问题可以借助函数思想来探讨,具体步骤:第一步,确定变量;第二步:在直角坐标系中画出函数图象;第三步:根据函数图象猜想并求出函数关系式;第四步:把另外的某一点代入验证,若成立,则用这个关系式去求解.
解决问题:
根据以上步骤,请你解答“问题情境”.
一学校为了绿化校园环境,向某园林公司购买力一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?
如图,AD是△ABC的角平分线,过点D作DE∥AB,DF∥AC,分别交AC、AB于点E和F.在图中画出线段DE和DF;
连接EF,则线段AD和EF互相垂直平分,这是为什么?

如图,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).求证:△ACD∽△BAC;
求DC的长;
设四边形AFEC的面积为y,求y 关于t的函数关系式,并求出y的最小值.