..如图,某小区准备在一直角围墙 内的空地上植造“绿地
内的空地上植造“绿地 ”,其中
”,其中 ,
,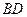 长可根据需要进行调节(
长可根据需要进行调节(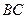 足够长),现规划在
足够长),现规划在 内接正方形
内接正方形 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积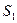 与种花的面积
与种花的面积 的比
的比 为
为 ,
,
(1)设角 ,将
,将 表示成
表示成 的函数关系;
的函数关系;
(2)当 为多长时,
为多长时, 有最小值,最小值是多少?
有最小值,最小值是多少?
已知 函数
函数 .
.
(1)求函数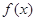 的最小正周期和对称轴的方程;
的最小正周期和对称轴的方程;
(2)设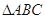 的角
的角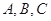 的对边分别为
的对边分别为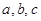 ,且
,且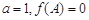 ,求
,求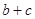 的取值范围.
的取值范围.
已知函数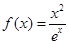 ,
,
(1)求函数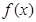 的单调区间;
的单调区间;
(2)若方程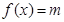 有且只有一个解,求实数m的取值范围;
有且只有一个解,求实数m的取值范围;
(3)当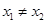 且
且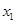 ,
,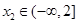 时,若有
时,若有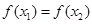 ,求证:
,求证: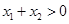 .
.
已知直线 过点
过点 且与抛物线
且与抛物线 交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
(1)求抛物线的标准方程;
(2)设 是直线
是直线 上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
上任意一点,求证:直线QA、QM、QB的斜率依次成等差数列.
在1和2之间依次插入n 个正数
个正数 使得这
使得这 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这 个数的乘积记作
个数的乘积记作 ,令
,令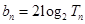 .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)令 ,设
,设 ,求
,求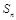 .
.
在如图所示的几何体中,四边形ABCD为正方形, 为直角三角形,
为直角三角形, ,且
,且 .
.
(1)证明:平面 平面
平面 ;
;
(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.