三、解答题：（本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．）
16. （本小题满分12分）
已知向量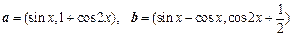
，定义函数
（Ⅰ）求函数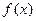
最小正周期；
（Ⅱ）在△ABC中,角A为锐角，且
，求边AC的长．
（本小题满分10分）选修4～5：不等式选讲
设不等式－2<|x－1|－|x＋2|<0的解集为M，a，b∈M．
（1）证明：
；
（2）比较|1－4ab|与2|a－b|的大小，并说明理由．
（本小题满分10分）选修4～4：坐标系与参数方程
在直角坐标系xOy中，直线l的参数方程为
（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴）中，圆C的方程为r=6sinq．
（1）求圆C的直角坐标方程；
（2）若点P（1，2），设圆C与直线l交于点A，B．求∣PA∣+∣PB∣的最小值．
（本小题满分10分）选修4～1:几何证明选讲
如图，AB是⊙O的一条切线，切点为B，直线ADE，CFD，CGE都是⊙O的割线，已知AC=AB．
（1）若CG=1，CD=4，求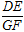
的值；
（2）求证：FG//AC．
（本小题满分12分）已知函数f（x）＝
（e为自然对数的底数）．
（1）若a<1，求函数f（x）的单调区间；
（2）若a=1，函数φ（x）＝xf（x）＋t f ′（x）＋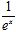
，存在实数x1，x2∈[0，1]，使 2φ（x1）<φ（x2）成立，求实数t的取值范围．
（本小题满分12分）己知A、B、C是椭圆C：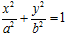
（a>b>0）上的三点，其中点A的坐标为
，BC 过椭圆的中心，且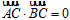
，
．
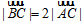（1）求椭圆C的方程；
（2）过点（0，t）的直线l（斜率存在时）与椭圆C交于P，Q两点，设D为椭圆C与y轴负半轴的交点，且
，求实数t的取值范围．