(本小题满分12分)已知函数f(x)= (e为自然对数的底数).
(e为自然对数的底数).
(1)若a<1,求函数f(x)的单调区间;
(2)若a=1,函数φ(x)=xf(x)+t f ′(x)+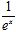 ,存在实数x1,x2∈[0,1],使 2φ(x1)<φ(x2)成立,求实数t的取值范围.
,存在实数x1,x2∈[0,1],使 2φ(x1)<φ(x2)成立,求实数t的取值范围.
如图,圆O与离心率为 的椭圆T:
的椭圆T: (
(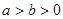 )相切于点M
)相切于点M 。
。
⑴求椭圆T与圆O的方程;
⑵过点M引两条互相垂直的两直线 、
、 与两曲线分别交于点A、C与点B、D(均不重合)。
与两曲线分别交于点A、C与点B、D(均不重合)。
①若P为椭圆上任一点,记点P到两直线的距离分别为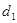 、
、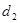 ,求
,求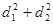 的最大值;
的最大值;
②若 ,求
,求 与
与 的方程。
的方程。
如图,在海岸线一侧C处有一个美丽的小岛,某旅游公司为方便游客,在上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米。公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛。据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元。设∠ ,每批游客从各自报名点到C岛所需运输成本S元。
,每批游客从各自报名点到C岛所需运输成本S元。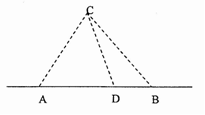
⑴写出S关于 的函数表达式,并指出
的函数表达式,并指出 的取值范围;
的取值范围;
⑵问中转点D距离A处多远时,S最小?
如图的几何体中,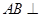 平面
平面 ,
, 平面
平面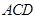 ,△
,△ 为等边三角形,
为等边三角形,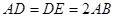 ,
,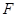 为
为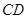 的中点.
的中点.
(1)求证: 平面
平面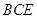 ;
;
(2)求证:平面 平面
平面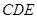 .
.
在三角形ABC中,已知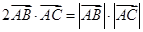 ,设∠CAB=α,
,设∠CAB=α,
(1)求角α的值;
(2)若 ,其中
,其中 ,求
,求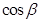 的值.
的值.
设函数f(x)=|2x-1|+|2x-3|,x∈R
(Ⅰ)解不等式f(x)≤5;
(Ⅱ)若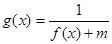 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.