已知向量 =(6,2),
=(6,2),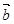 =(-3,k),当k为何值时,有
=(-3,k),当k为何值时,有
(1), ∥
∥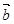 ?(2),
?(2), ⊥
⊥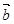 ?(3),
?(3), 与
与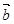 所成角θ是钝角 ?
所成角θ是钝角 ?
对于给定数列 ,如果存在实常数
,如果存在实常数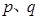 ,使得
,使得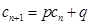 对于任意
对于任意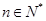 都成立,我们称数列
都成立,我们称数列 是 “
是 “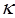 类数列”.
类数列”.
(Ⅰ)若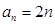 ,
,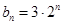 ,
,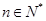 ,数列
,数列 、
、 是否为“
是否为“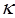 类数列”?若是,指出它对应的实常数
类数列”?若是,指出它对应的实常数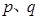 ,若不是,请说明理由;
,若不是,请说明理由;
(Ⅱ)证明:若数列 是“
是“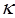 类数列”,则数列
类数列”,则数列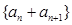 也是“
也是“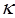 类数列”;
类数列”;
(Ⅲ)若数列 满足
满足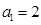 ,
, ,
, 为常数.求数列
为常数.求数列 前2012项的和.并判断
前2012项的和.并判断 是否为“
是否为“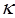 类数列”,说明理由.
类数列”,说明理由.
已知椭圆 (
( )过点
)过点 (0,2),离心率
(0,2),离心率 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过定点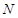 (2,0)的直线
(2,0)的直线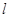 与椭圆相交于
与椭圆相交于 两点,且
两点,且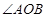 为锐角(其中
为锐角(其中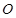 为坐标原点),求直线
为坐标原点),求直线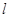 倾斜角的取值范围.
倾斜角的取值范围.
已知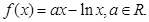
(Ⅰ)当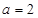 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若 在
在 处有极值,求
处有极值,求 的单调递增区间;
的单调递增区间;
(Ⅲ)是否存在实数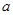 ,使
,使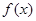 在区间
在区间 的最小值是3,若存在,求出
的最小值是3,若存在,求出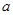 的值;
的值;
若不存在,说明理由.
如图,矩形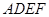 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直,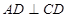 ,
,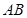 ∥
∥ ,
, ,
, ,
,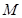 为
为 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面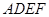 ;
;
(Ⅱ)求证:平面
 平面
平面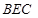 ;
;
(Ⅲ)若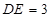 ,求平面
,求平面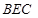 与平面
与平面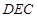 所成锐二面角的余弦值.
所成锐二面角的余弦值.