如图,矩形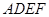 与梯形
与梯形 所在的平面互相垂直,
所在的平面互相垂直,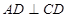 ,
,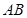 ∥
∥ ,
, ,
, ,
,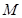 为
为 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面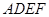 ;
;
(Ⅱ)求证:平面
 平面
平面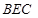 ;
;
(Ⅲ)若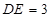 ,求平面
,求平面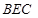 与平面
与平面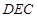 所成锐二面角的余弦值.
所成锐二面角的余弦值.
已知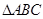 中,角
中,角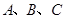 的对边分别为
的对边分别为 ,且有
,且有 .
.
(1)求角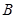 的大小;
的大小;
(2)设向量 ,且
,且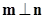 ,求
,求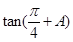 的值.
的值.
已知数列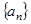 的各项均是正数,其前
的各项均是正数,其前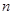 项和为
项和为 ,满足
,满足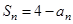 .
.
(I)求数列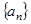 的通项公式;
的通项公式;
(II)设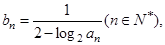 数列
数列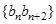 的前
的前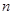 项和为
项和为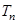 ,求证:
,求证: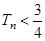 .
.
已知函数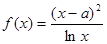 (其中
(其中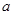 为常数).
为常数).
(Ⅰ)当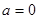 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)当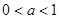 时,设函数
时,设函数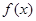 的3个极值点为
的3个极值点为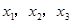 ,且
,且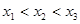 .证明:
.证明: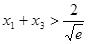 .
.
已知函数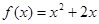 .
.
(Ⅰ)若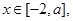 求
求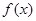 的值域;
的值域;
(Ⅱ)若存在实数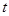 ,当
,当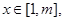
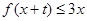 恒成立,求实数
恒成立,求实数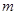 的取值范围.
的取值范围.
成都市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰。若现有500人参加测试,学生成绩的频率分布直方图如下: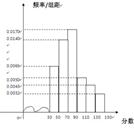
(I)求获得参赛资格的人数;
(II)根据频率直方图,估算这500名学生测试的平均成绩;
(III)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为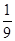 ,求甲在初赛中答题个数的分布列及数学期望.
,求甲在初赛中答题个数的分布列及数学期望.