(本小题12分)
已知数列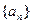 的前项和为
的前项和为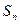 ,
,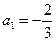 ,
,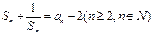
(1)求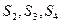
(2)猜想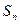 的表
的表 达式,并用数学归纳法证明。
达式,并用数学归纳法证明。
(本小题满分13分)已知二次函数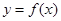 的图象的顶点坐标为
的图象的顶点坐标为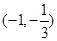 ,且过坐标原点
,且过坐标原点 .数列
.数列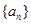 的前
的前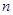 项和为
项和为 ,点
,点 在二次函数
在二次函数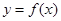 的图象上.
的图象上.
(Ⅰ)求数列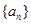 的通项公式;
的通项公式;
(Ⅱ)设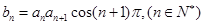 ,数列
,数列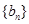 的前
的前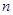 项和为
项和为 ,若
,若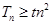 对
对 恒成立,求实数
恒成立,求实数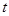 的取值范围;
的取值范围;
(Ⅲ)在数列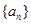 中是否存在这样一些项:
中是否存在这样一些项: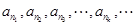

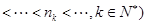 ,这些项都能够构成以
,这些项都能够构成以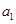 为首项,
为首项, 为公比的等比数列
为公比的等比数列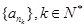 ?若存在,写出
?若存在,写出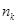 关于
关于 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
(本小题满分14分)已知椭圆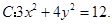
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)设椭圆 上在第二象限的点
上在第二象限的点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线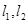 与椭圆
与椭圆 的另一交点分别为
的另一交点分别为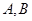 .且
.且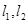 的斜率互为相反数,
的斜率互为相反数,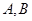 两点关于坐标原点
两点关于坐标原点 的对称点分别为
的对称点分别为 ,求四边形
,求四边形 的面积的最大值.
的面积的最大值.
(本小题满分13分)已知函数 .
.
(Ⅰ)当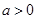 时,求函数
时,求函数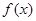 的单调区间;
的单调区间;
(Ⅱ)设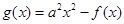 ,且函数
,且函数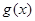 在点
在点 处的切线为
处的切线为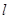 ,直线
,直线 //
//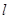 ,且
,且 在
在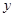 轴上的截距为1.求证:无论
轴上的截距为1.求证:无论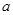 取任何实数,函数
取任何实数,函数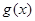 的图象恒在直线
的图象恒在直线 的下方.
的下方.
(本小题满分14分)如图,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, //
// ,
, ,平面
,平面 底面
底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点,

(Ⅰ)求证: ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题满分13分)
某农民在一块耕地上种植一种作物,每年种植成本为 元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
(Ⅰ)设 表示该农民在这块地上种植1年此作物的利润,求
表示该农民在这块地上种植1年此作物的利润,求 的分布列;
的分布列;
(Ⅱ)若在这块地上连续3年种植此作物,求这3年中第二年的利润少于第一年的概率.