[应用题]如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一绳子的两端拴于立柱与铁杠结合处,绳子自然下垂呈抛物线状.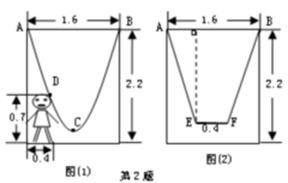
(1)如图(1)一身高为0.7米的小孩站在离立柱0.4米处,其头部刚好触到绳子,求绳子最低点到地面的距离;
(2)如图(2),为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4米的木板.除掉系木板用去的绳子后,两边的绳子长正好各为2米,木板与地面平行.求这时木板离地面的距离(参考数据: ≈1.8,
≈1.8, 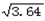 ≈1.9,
≈1.9, 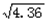 ≈2.1).
≈2.1).
(11·西宁)(本小题满分10分)国家发改委公布的《商品房销售明码标价规定》,从2011年5月1日起商品房销售实行一套一标价.商品房销售价格明码标价后,可以自行降价、打折销售,但涨价必须重新申报.某市某楼盘准备以每平方米5000元的均价对外销售,由于新政策的出台,购房都持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套100平方米的房子,开发商还给予以下两种优惠方案发供选择:
①打9.8折销售;②不打折,送两年物业管理费,物业管理费是每平方米每月1.5元,请问哪种方案更优惠?
已知:如图,BD为⊙O的直径,AB=AC,AD交BC与E,AE=2,ED=4.
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使BF=OB,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
如图,阅读对话,解答问题.
盒子中有三个除数字外完全相同的小球—1,1,2.
小兵:我蒙上眼睛,先从盒子中摸出一个小球(摸出后不放回),用P表示我摸出小球上标有的数字.
小红:你摸出后,我也蒙上眼睛,再从盒子中摸出一个小球,用Q表示我摸出小球上标有的数字.
(1)试用树形图或列表法写出满足关于x的方程x2+px+q=0的所有等可能结果;
(2)求(1)中方程有实数根的概率.
(11·西宁)(本小题满分8分)国家教育部规定“中小学生每天在校体育活动时间不少于1小时”.西宁市某中学为了了解学生体育活动的情况,随 机抽查了520名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”.以下是根据所得的数据制成的统计图的一部分.
机抽查了520名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”.以下是根据所得的数据制成的统计图的一部分.
根据以上信息,解答下列问题:
(1)随机抽查的学生中每天在校锻炼时间超过1小时的人数是_▲;
(2)请 将图14补充完整;
将图14补充完整;
(3)2011年我市初中应届毕业生约为11000人,请你估计今年全市初中应届毕业生中每天锻炼时间超过1小时的学生约有多少人?
11·西宁)(本小题满分8分)如图12 ,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
(1)求证:四边形AODE是菱形;
(2).若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,
其余条件不变,则四边形AODE是_▲.